data wrangling and summaries
Data wrangling refers to the process of organizing, cleaning up, and making a “raw” data set more ready for downstream analysis. It is a key piece of any data analysis process. Here we will look at a few different aspects of wrangling, including data import, subsetting, pivoting, and summarizing data.
data import
To analyze data that is stored on your own computer you can indeed import it into RStudio.
The easiest way to do this is to use the interactive command readCSV(), a function that comes with the phylochemistry source command. You run readCSV() in your console, then navigate to the data on your hard drive.
Another option is to read the data in from a path. For this, you will need to know the “path” to your data file. This is essentially the street address of your data on your computer’s hard drive. Paths look different on Mac and PC.
- On Mac:
/Users/lucasbusta/Documents/sample_data_set.csv(note the forward slashes!) - On PC:
C:\\My Computer\\Documents\\sample_data_set.csv(note double backward slashes!)
You can quickly find paths to files via the following:
- On Mac: Locate the file in Finder. Right-click on the file, hold the Option key, then click “Copy
as Pathname” - On PC: Locate the file in Windows Explorer. Hold down the Shift key then right-click on the file. Click “Copy As Path”
With these paths, we can read in data using the read_csv command. We’ll run read_csv("<path_to_your_data>"). Note the use of QUOTES ""! Those are necessary. Also make sure your path uses the appropriate direction of slashes for your operating system.
subsetting
So far, we have always been passing whole data sets to ggplot to do our plotting. However, suppose we wanted to get at just certain portions of our dataset, say, specific columns, or specific rows? Here are a few ways to do that:
# To look at a single column (the third column)
head(alaska_lake_data[,3])
## # A tibble: 6 × 1
## water_temp
## <dbl>
## 1 6.46
## 2 6.46
## 3 6.46
## 4 6.46
## 5 6.46
## 6 6.46
# To look at select columns:
head(alaska_lake_data[,2:5])
## # A tibble: 6 × 4
## park water_temp pH element
## <chr> <dbl> <dbl> <chr>
## 1 BELA 6.46 7.69 C
## 2 BELA 6.46 7.69 N
## 3 BELA 6.46 7.69 P
## 4 BELA 6.46 7.69 Cl
## 5 BELA 6.46 7.69 S
## 6 BELA 6.46 7.69 F
# To look at a single row (the second row)
head(alaska_lake_data[2,])
## # A tibble: 1 × 7
## lake park water_temp pH element mg_per_L element_type
## <chr> <chr> <dbl> <dbl> <chr> <dbl> <chr>
## 1 Devi… BELA 6.46 7.69 N 0.028 bound
# To look at select rows:
head(alaska_lake_data[2:5,])
## # A tibble: 4 × 7
## lake park water_temp pH element mg_per_L element_type
## <chr> <chr> <dbl> <dbl> <chr> <dbl> <chr>
## 1 Devi… BELA 6.46 7.69 N 0.028 bound
## 2 Devi… BELA 6.46 7.69 P 0 bound
## 3 Devi… BELA 6.46 7.69 Cl 10.4 free
## 4 Devi… BELA 6.46 7.69 S 0.62 free
# To look at just a single column, by name
head(alaska_lake_data$pH)
## [1] 7.69 7.69 7.69 7.69 7.69 7.69
# To look at select columns by name
head(select(alaska_lake_data, park, water_temp))
## # A tibble: 6 × 2
## park water_temp
## <chr> <dbl>
## 1 BELA 6.46
## 2 BELA 6.46
## 3 BELA 6.46
## 4 BELA 6.46
## 5 BELA 6.46
## 6 BELA 6.46wide and long data
When we make data tables by hand, it’s often easy to make a wide-style table like the following. In it, the abundances of 7 different fatty acids in 10 different species are tabulated. Each fatty acid gets its own row, each species, its own column.
head(fadb_sample)
## # A tibble: 6 × 11
## fatty_acid Agonandra_brasiliensis Agonandra_silvatica
## <chr> <dbl> <dbl>
## 1 Hexadecanoic a… 3.4 1
## 2 Octadecanoic a… 6.2 0.1
## 3 Eicosanoic acid 4.7 3.5
## 4 Docosanoic acid 77.4 0.4
## 5 Tetracosanoic … 1.4 1
## 6 Hexacosanoic a… 1.9 12.6
## # ℹ 8 more variables: Agonandra_excelsa <dbl>,
## # Heisteria_silvianii <dbl>, Malania_oleifera <dbl>,
## # Ximenia_americana <dbl>, Ongokea_gore <dbl>,
## # Comandra_pallida <dbl>, Buckleya_distichophylla <dbl>,
## # Nuytsia_floribunda <dbl>While this format is very nice for filling in my hand (such as in a lab notebook or similar), it does not groove with ggplot and other tidyverse functions very well. We need to convert it into a long-style table. This is done using pivot_longer(). You can think of this function as transforming both your data’s column names (or some of the column names) and your data matrix’s values (in this case, the measurements) each into their own variables (i.e. columns). We can do this for our fatty acid dataset using the command below. In it, we specify what data we want to transform (data = fadb_sample), we need to tell it what columns we want to transform (cols = 2:11), what we want the new variable that contains column names to be called (names_to = "plant_species") and what we want the new variable that contains matrix values to be called (values_to = "relative_abundance"). All together now:
pivot_longer(data = fadb_sample, cols = 2:11, names_to = "plant_species", values_to = "relative_abundance")
## # A tibble: 70 × 3
## fatty_acid plant_species relative_abundance
## <chr> <chr> <dbl>
## 1 Hexadecanoic acid Agonandra_brasilien… 3.4
## 2 Hexadecanoic acid Agonandra_silvatica 1
## 3 Hexadecanoic acid Agonandra_excelsa 1.2
## 4 Hexadecanoic acid Heisteria_silvianii 2.9
## 5 Hexadecanoic acid Malania_oleifera 0.7
## 6 Hexadecanoic acid Ximenia_americana 3.3
## 7 Hexadecanoic acid Ongokea_gore 1
## 8 Hexadecanoic acid Comandra_pallida 2.3
## 9 Hexadecanoic acid Buckleya_distichoph… 1.6
## 10 Hexadecanoic acid Nuytsia_floribunda 3.8
## # ℹ 60 more rowsBrilliant! Now we have a long-style table that can be used with ggplot.
the pipe (%>%)
We have seen how to create new objects using <-, and we have been filtering and plotting data using, for example:
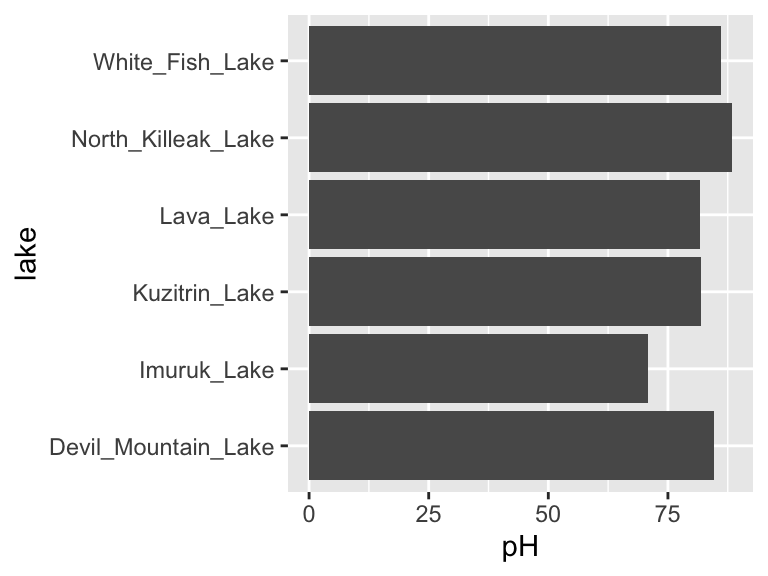
However, as our analyses get more complex, the code can get long and hard to read. We’re going to use the pipe %>% to help us with this. Check it out:
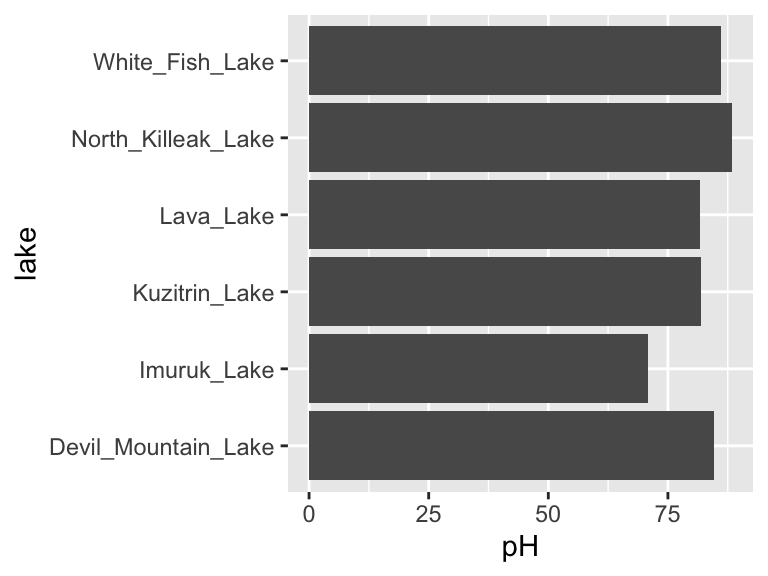
Neat! Another way to think about the pipe:
The pipe will become more important as our analyses become more sophisticated, which happens very quickly when we start working with summary statistics, as we shall now see…
summary statistics
So far, we have been plotting raw data. This is well and good, but it is not always suitable. Often we have scientific questions that cannot be answered by looking at raw data alone, or sometimes there is too much raw data to plot. For this, we need summary statistics - things like averages, standard deviations, and so on. While these metrics can be computed in Excel, programming such can be time consuming, especially for group statistics. Consider the example below, which uses the ny_trees dataset. The NY Trees dataset contains information on nearly half a million trees in New York City (this is after considerable filtering and simplification):
head(ny_trees)
## # A tibble: 6 × 14
## tree_height tree_diameter address tree_loc pit_type
## <dbl> <dbl> <chr> <chr> <chr>
## 1 21.1 6 1139 57 STREET Front Sidewal…
## 2 59.0 6 2220 BERGEN A… Across Sidewal…
## 3 92.4 13 2254 BERGEN A… Across Sidewal…
## 4 50.2 15 2332 BERGEN A… Across Sidewal…
## 5 95.0 21 2361 EAST 7… Front Sidewal…
## 6 67.5 19 2409 EAST 7… Front Continu…
## # ℹ 9 more variables: soil_lvl <chr>, status <chr>,
## # spc_latin <chr>, spc_common <chr>, trunk_dmg <chr>,
## # zipcode <dbl>, boroname <chr>, latitude <dbl>,
## # longitude <dbl>More than 300,000 observations of 14 variables! That’s 4.2M data points! Now, what is the average and standard deviation of the height and diameter of each tree species within each NY borough? Do those values change for trees that are in parks versus sidewalk pits?? I don’t even know how one would begin to approach such questions using traditional spreadsheets. Here, we will answer these questions with ease using two new commands: group_by() and summarize(). Let’s get to it.
Say that we want to know (and of course, visualize) the mean and standard deviation of the heights of each tree species in NYC. We can see that data in first few columns of the NY trees dataset above, but how to calculate these statistics? In R, mean can be computed with mean() and standard deviation can be calculated with sd(). We will use the function summarize() to calculate summary statistics. So, we can calculate the average and standard deviation of all the trees in the data set as follows:
ny_trees %>%
summarize(mean_height = mean(tree_height))
## # A tibble: 1 × 1
## mean_height
## <dbl>
## 1 72.6
ny_trees %>%
summarize(stdev_height = sd(tree_height))
## # A tibble: 1 × 1
## stdev_height
## <dbl>
## 1 28.7Great! But how to do this for each species? We need to subdivide the data by species, then compute the mean and standard deviation, then recombine the results into a new table. First, we use group_by(). Note that in ny_trees, species are indicated in the column called spc_latin. Once the data is grouped, we can use summarize() to compute statistics.
ny_trees %>%
group_by(spc_latin) %>%
summarize(mean_height = mean(tree_height))
## # A tibble: 12 × 2
## spc_latin mean_height
## <chr> <dbl>
## 1 ACER PLATANOIDES 82.6
## 2 ACER RUBRUM 106.
## 3 ACER SACCHARINUM 65.6
## 4 FRAXINUS PENNSYLVANICA 60.6
## 5 GINKGO BILOBA 90.4
## 6 GLEDITSIA TRIACANTHOS 53.0
## 7 PLATANUS ACERIFOLIA 82.0
## 8 PYRUS CALLERYANA 21.0
## 9 QUERCUS PALUSTRIS 65.5
## 10 QUERCUS RUBRA 111.
## 11 TILIA CORDATA 98.8
## 12 ZELKOVA SERRATA 101.Bam. Mean height of each tree species. We can also count the number of observations using n():
ny_trees %>%
group_by(spc_latin) %>%
summarize(number_of_individuals = n())
## # A tibble: 12 × 2
## spc_latin number_of_individuals
## <chr> <int>
## 1 ACER PLATANOIDES 67260
## 2 ACER RUBRUM 11506
## 3 ACER SACCHARINUM 13161
## 4 FRAXINUS PENNSYLVANICA 16987
## 5 GINKGO BILOBA 15672
## 6 GLEDITSIA TRIACANTHOS 48707
## 7 PLATANUS ACERIFOLIA 80075
## 8 PYRUS CALLERYANA 39125
## 9 QUERCUS PALUSTRIS 37058
## 10 QUERCUS RUBRA 10020
## 11 TILIA CORDATA 25970
## 12 ZELKOVA SERRATA 13221Cool! summarize() is more powerful though, we can do many summary statistics at once:
ny_trees %>%
group_by(spc_latin) %>%
summarize(
mean_height = mean(tree_height),
stdev_height = sd(tree_height)
) -> ny_trees_by_spc_summ
ny_trees_by_spc_summ
## # A tibble: 12 × 3
## spc_latin mean_height stdev_height
## <chr> <dbl> <dbl>
## 1 ACER PLATANOIDES 82.6 17.6
## 2 ACER RUBRUM 106. 15.7
## 3 ACER SACCHARINUM 65.6 16.6
## 4 FRAXINUS PENNSYLVANICA 60.6 21.3
## 5 GINKGO BILOBA 90.4 24.5
## 6 GLEDITSIA TRIACANTHOS 53.0 13.0
## 7 PLATANUS ACERIFOLIA 82.0 16.0
## 8 PYRUS CALLERYANA 21.0 5.00
## 9 QUERCUS PALUSTRIS 65.5 6.48
## 10 QUERCUS RUBRA 111. 20.7
## 11 TILIA CORDATA 98.8 32.6
## 12 ZELKOVA SERRATA 101. 10.7Now we can use this data in plotting. For this, we will use a new geom, geom_pointrange, which takes x and y aesthetics, as usual, but also requires two additional y-ish aesthetics ymin and ymax (or xmin and xmax if you want them to vary along x). Also, note that in the aesthetic mappings for xmin and xmax, we can use a mathematical expression: mean-stdev and mean+stdev, respectivey. In our case, these are mean_height - stdev_height and mean_height + stdev_height. Let’s see it in action:
ny_trees_by_spc_summ %>%
ggplot() +
geom_pointrange(
aes(
y = spc_latin,
x = mean_height,
xmin = mean_height - stdev_height,
xmax = mean_height + stdev_height
)
)
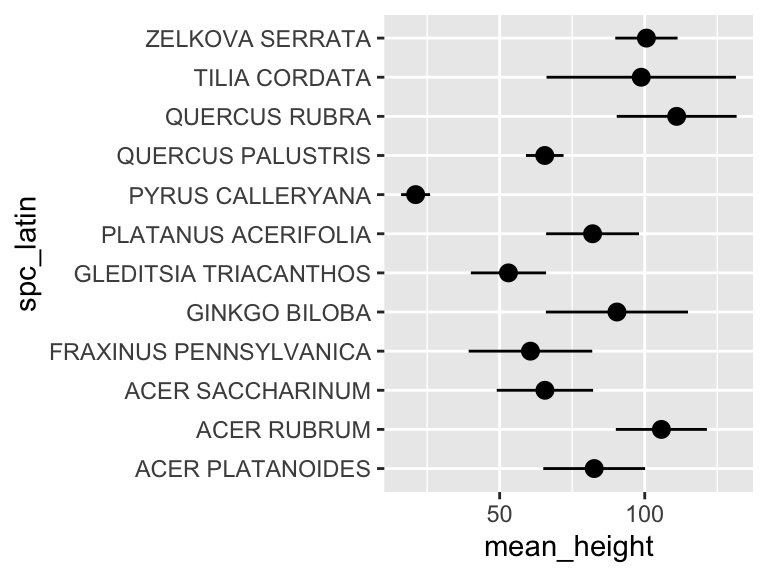
Cool! Just like that, we’ve found (and visualized) the average and standard deviation of tree heights, by species, in NYC. But it doesn’t stop there. We can use group_by() and summarize() on multiple variables (i.e. more groups). We can do this to examine the properties of each tree species in each NYC borough. Let’s check it out:
ny_trees %>%
group_by(spc_latin, boroname) %>%
summarize(
mean_diam = mean(tree_diameter),
stdev_diam = sd(tree_diameter)
) -> ny_trees_by_spc_boro_summ
ny_trees_by_spc_boro_summ
## # A tibble: 48 × 4
## # Groups: spc_latin [12]
## spc_latin boroname mean_diam stdev_diam
## <chr> <chr> <dbl> <dbl>
## 1 ACER PLATANOIDES Bronx 13.9 6.74
## 2 ACER PLATANOIDES Brooklyn 15.4 14.9
## 3 ACER PLATANOIDES Manhattan 11.6 8.45
## 4 ACER PLATANOIDES Queens 15.1 12.9
## 5 ACER RUBRUM Bronx 11.4 7.88
## 6 ACER RUBRUM Brooklyn 10.5 7.41
## 7 ACER RUBRUM Manhattan 6.63 4.23
## 8 ACER RUBRUM Queens 14.1 8.36
## 9 ACER SACCHARINUM Bronx 19.7 10.5
## 10 ACER SACCHARINUM Brooklyn 22.2 10.1
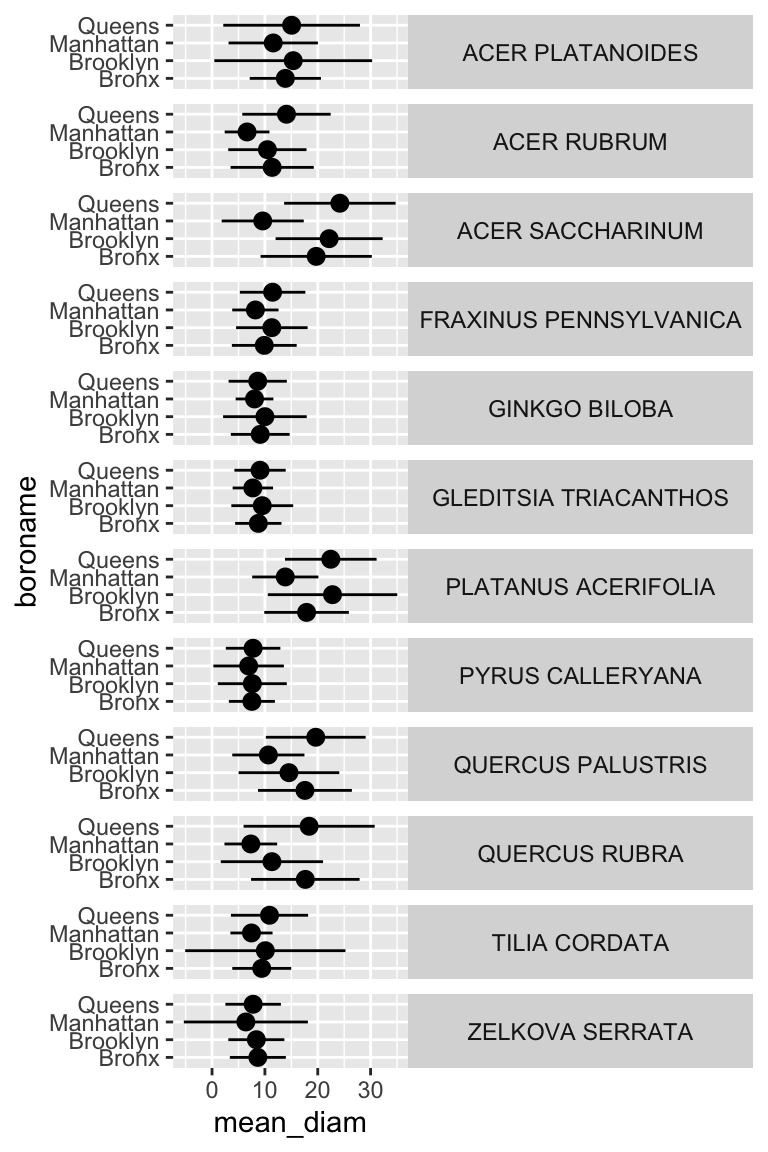
## # ℹ 38 more rowsNow we have summary statistics for each tree species within each borough. This is different from the previous plot in that we now have an additional variable (boroname) in our summarized dataset. This additional variable needs to be encoded in our plot. Let’s map boroname to x and facet over tree species, which used to be on x. We’ll also manually modify the theme element strip.text.y to get the species names in a readable position.
ny_trees_by_spc_boro_summ %>%
ggplot() +
geom_pointrange(
aes(
y = boroname,
x = mean_diam,
xmin = mean_diam-stdev_diam,
xmax = mean_diam+stdev_diam
)
) +
facet_grid(spc_latin~.) +
theme(
strip.text.y = element_text(angle = 0)
)
Excellent! And if we really want to go for something pretty:
ny_trees_by_spc_boro_summ %>%
ggplot() +
geom_pointrange(
aes(
y = boroname,
x = mean_diam,
xmin = mean_diam-stdev_diam,
xmax = mean_diam+stdev_diam,
fill = spc_latin
), color = "black", shape = 21
) +
labs(
y = "Borough",
x = "Trunk diameter"
# caption = str_wrap("Figure 1: Diameters of trees in New York City. Points correspond to average diameters of each tree species in each borough. Horizontal lines indicate the standard deviation of tree diameters. Points are colored according to tree species.", width = 80)
) +
facet_grid(spc_latin~.) +
guides(fill = "none") +
scale_fill_brewer(palette = "Paired") +
theme_bw() +
theme(
strip.text.y = element_text(angle = 0),
plot.caption = element_text(hjust = 0.5)
)
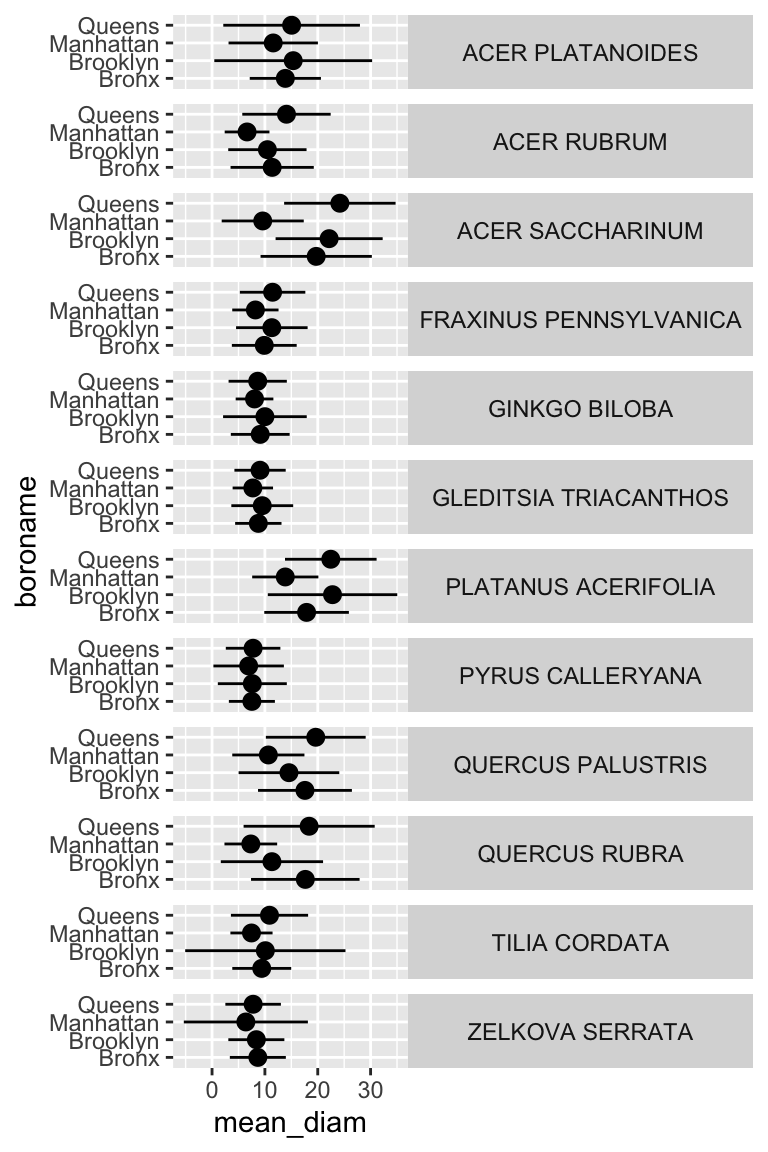
Now we are getting somewhere. It looks like there are some really big maple trees (Acer) in Queens.
ordering
We can also sort or order a data frame based on a specific column with the command arrange(). Let’s have a quick look. Suppose we wanted to know which lake was the coldest:
arrange(alaska_lake_data, water_temp)
## # A tibble: 220 × 7
## lake park water_temp pH element mg_per_L
## <chr> <chr> <dbl> <dbl> <chr> <dbl>
## 1 Desperation_Lake NOAT 2.95 6.34 C 2.1
## 2 Desperation_Lake NOAT 2.95 6.34 N 0.005
## 3 Desperation_Lake NOAT 2.95 6.34 P 0
## 4 Desperation_Lake NOAT 2.95 6.34 Cl 0.2
## 5 Desperation_Lake NOAT 2.95 6.34 S 2.73
## 6 Desperation_Lake NOAT 2.95 6.34 F 0.01
## 7 Desperation_Lake NOAT 2.95 6.34 Br 0
## 8 Desperation_Lake NOAT 2.95 6.34 Na 1.11
## 9 Desperation_Lake NOAT 2.95 6.34 K 0.16
## 10 Desperation_Lake NOAT 2.95 6.34 Ca 5.87
## # ℹ 210 more rows
## # ℹ 1 more variable: element_type <chr>Or suppose we wanted to know which was the warmest?
arrange(alaska_lake_data, desc(water_temp))
## # A tibble: 220 × 7
## lake park water_temp pH element mg_per_L
## <chr> <chr> <dbl> <dbl> <chr> <dbl>
## 1 Lava_Lake BELA 20.2 7.42 C 8.3
## 2 Lava_Lake BELA 20.2 7.42 N 0.017
## 3 Lava_Lake BELA 20.2 7.42 P 0.001
## 4 Lava_Lake BELA 20.2 7.42 Cl 2.53
## 5 Lava_Lake BELA 20.2 7.42 S 0.59
## 6 Lava_Lake BELA 20.2 7.42 F 0.04
## 7 Lava_Lake BELA 20.2 7.42 Br 0.01
## 8 Lava_Lake BELA 20.2 7.42 Na 2.93
## 9 Lava_Lake BELA 20.2 7.42 K 0.57
## 10 Lava_Lake BELA 20.2 7.42 Ca 11.8
## # ℹ 210 more rows
## # ℹ 1 more variable: element_type <chr>arrange() will work on grouped data, which is particularly useful in combination with slice(), which can show us the first n elements in each group:
alaska_lake_data %>%
group_by(park) %>%
arrange(water_temp) %>%
slice(1)
## # A tibble: 3 × 7
## # Groups: park [3]
## lake park water_temp pH element mg_per_L element_type
## <chr> <chr> <dbl> <dbl> <chr> <dbl> <chr>
## 1 Devi… BELA 6.46 7.69 C 3.4 bound
## 2 Wild… GAAR 5.5 6.98 C 6.5 bound
## 3 Desp… NOAT 2.95 6.34 C 2.1 boundIt looks like the coldest lakes in the three parks are Devil Mountain Lake, Wild Lake, and Desperation Lake!
mutate
One last thing before our exercises… there is another command called mutate(). It is like summarize it calculates user-defined statistics, but it creates output on a per-observation level instead of for each group. This means that it doesn’t make the data set smaller, in fact it makes it bigger, by creating a new row for the new variables defined inside mutate(). It can also take grouped data. This is really useful for calculating percentages within groups. For example: within each park, what percent of the park’s total dissolved sulfur does each lake have?
alaska_lake_data %>%
filter(element == "S") %>%
group_by(park) %>%
select(lake, park, element, mg_per_L) %>%
mutate(percent_S = mg_per_L/sum(mg_per_L)*100)
## # A tibble: 20 × 5
## # Groups: park [3]
## lake park element mg_per_L percent_S
## <chr> <chr> <chr> <dbl> <dbl>
## 1 Devil_Mountain_Lake BELA S 0.62 32.3
## 2 Imuruk_Lake BELA S 0.2 10.4
## 3 Kuzitrin_Lake BELA S 0.29 15.1
## 4 Lava_Lake BELA S 0.59 30.7
## 5 North_Killeak_Lake BELA S 0.04 2.08
## 6 White_Fish_Lake BELA S 0.18 9.38
## 7 Iniakuk_Lake GAAR S 12.1 13.2
## 8 Kurupa_Lake GAAR S 12.4 13.6
## 9 Lake_Matcharak GAAR S 13.3 14.5
## 10 Lake_Selby GAAR S 7.92 8.64
## 11 Nutavukti_Lake GAAR S 2.72 2.97
## 12 Summit_Lake GAAR S 3.21 3.50
## 13 Takahula_Lake GAAR S 5.53 6.03
## 14 Walker_Lake GAAR S 5.77 6.30
## 15 Wild_Lake GAAR S 28.7 31.3
## 16 Desperation_Lake NOAT S 2.73 25.8
## 17 Feniak_Lake NOAT S 4.93 46.5
## 18 Lake_Kangilipak NOAT S 0.55 5.19
## 19 Lake_Narvakrak NOAT S 1.38 13.0
## 20 Okoklik_Lake NOAT S 1.01 9.53The percent columns for each park add to 100%, so, for example, Devil Mountain Lake has 32.3% of BELA’s dissolved sulfur.
exercises
Isn’t seven the most powerfully magical number? Isn’t seven the most powerfully magical number? Yes… I think the idea of a seven-part assignment would greatly appeal to an alchemist.
In this set of exercises we are going to use the periodic table. After you run source() you can load that data set using periodic_table. Please use that dataset to run analyses and answer the following questions/prompts. Compile the answers in an R Markdown document, compile it as a pdf, and upload it to the Canvas assignment. Please let me know if you have any questions. Good luck, and have fun!
Some pointers:
If your code goes off the page, please wrap it across multiple lines, as shown in some of the examples in the previous set of exercises.
Don’t be afraid to put the variable with the long elements / long text on the y-axis and the continuous variable on the x-axis.
If your axis tick labels are overlapping or not visible, do something to fix that. Some solutions could be: move the legend to the top of the plot (
theme(legend.position = "top")), rotate the text (theme(axis.text.x = element_text(angle = 90)), or make the text smaller (theme(axis.text.x = element_text(size = 8)).
Make a plot using
geom_point()that shows the average atomic weight of the elements discovered in each year spanned by the dataset (i.e. what was the average weight of the elements discovered in 1900? 1901? 1902? etc.). You should see a trend, particularly after 1950. What do you think has caused this trend?The column
state_at_RTindicates the state of each element at room temperate. Make a plot that shows the average first ionization potential of all the elements belonging to each state group indicated instate_at_RT(i.e. what is the average 1st ionization potential of all elements that are solid at room temp? liquid? etc.). Which is the highest?Filter the dataset so that only elements with atomic number less than 85 are included. Considering only these elements, what is the average and standard deviation of boiling points for each type of
crystal_structure? Make a plot usinggeom_pointrange()that shows the mean and standard deviation of each of these groups. What’s up with elements that have a cubic crystal structure?Now filter the original dataset so that only elements with atomic number less than 37 are considered. The elements in this dataset belong to the first four periods. What is the average abundance of each of these four periods in seawater? i.e. what is the average abundance of all elements from period 1? period 2? etc. Which period is the most abundant? In this context what does “CHON” mean? (not the rock band, though they are also excellent, especially that song that features GoYama)
Now filter the original dataset so that only elements with atomic number less than 103 are considered. Filter it further so that elements from group number 18 are excluded. Using this twice-filtered dataset, compute the average, minimum, and maximum values for electronegativiy for each
group_number. Usegeom_point()andgeom_errorbar()to illustrate the average, minimum, and maximum values for each group number.Filter the dataset so that only elements with atomic number less than 85 are considered. Group these by
color. Now filter out those that havecolor == "colorless". Of the remaining elements, which has the widest range of specific heats? Usegeom_point()andgeom_errorbar()to illustrate the mean and standard deviation of each color’s specific heats.You have learned many things in this course so far.
read_csv(),filter(),ggplot(), and nowgroup_by(),summarize(),mutate(),arrange(), andslice(). Using all these commands, create one or more graphics to illustrate what you consider to be one or more interesting trends in a data set of your own choosing. Use theme elements and scales to enhance your plot. Give your plot a nice caption based on the caption guide in this book.
further reading
Be sure to check out the Tidy Data Tutor: https://tidydatatutor.com/vis.html. An easy way to visualize what’s going on during data wrangling!