numerical models

model use

Next on our quest to develop our abilities in analytical data exploration is modeling. We will discuss two main ways to use numerical models: for inferential uses and predictive uses.

Inferential uses aim to understand and quantify the relationships between variables, focusing on the significance, direction, and strength of these relationships to draw conclusions about the data. When using inferential models we care a lot about the exact inner workings of the model because those inner workings are how we understand relationships between variables.
Predictive uses are designed with the primary goal of forecasting future outcomes or behaviors based on historical data. When using predictive models we often care much less about the exact inner workings of the model and instead care about accuracy. In other words, we don’t really care how the model works as long as it is accurate.

In the preceding section, we explored inferential models, highlighting the significance of grasping the quantitative aspects of the model’s mechanisms in order to understand relationships between variables. Now we will look at predictive models. Unlike inferential models, predictive models are typically more complex, often making it challenging to fully comprehend their internal processes. That is okay though, because when using predictive models we usually care most about their predictive accuracy, and are willing to sacrifice our quantitative understanding of the model’s inner workings to achieve higher accuracy.

Interestingly, increasingly complex predictive models do not always have higher accuracy. If a model is too complex we say that the model is ‘overfitted’ which means that the model is capturing noise and random fluctuations in the input data and using those erroneous patterns in its predictions. On the other hand, if a model is not complex enough then it will not be able to capture important true patterns in the data that are required to make accurate predictions. This means that we have to build models with the right level of complexity.

To build a model with the appropriate level of complexity we usually use this process: (i) separate out 80% of our data and call it the training data, (ii) build a series of models with varying complexity using the training data, (iii) use each of the models to make predictions about the remaining 20% of the data (the testing data), (iv) whichever model has the best predictive accuracy on the remaining 20% is the model with the appropriate level of complexity.

In this course, we will build both types of models using a function called buildModel. To use it, we simply give it our data, and tell it which to sets of values we want to compare. To tell it what we want to compare, we need to specify (at least) two things:

input_variables: the input variables (sometimes called “features” or “predictors”) the model should use as inputs for the prediction. Depending on the model, these could be continuous or categorical variables.
output_variable: the variable that the model should predict. Depending on the model, it could be a continuous value (regression) or a category/class (classification).

For model building, we also need to talk about handling missing data. If we have missing data in our data set, we need to one way forward is to impute it. This means that we need to fill in the missing values with something. There are many ways to do this, but we will use the median value of each column. We can do this using the impute function from the rstatix package. Let’s do that now:

any(is.na(metabolomics_data))
## [1] TRUE

metabolomics_data[] <- lapply(metabolomics_data, function(x) Hmisc::impute(x, median(x, na.rm = TRUE)))
any(is.na(metabolomics_data))
## [1] FALSE

single linear regression

We will start with some of the simplest models - linear models. There are a variety of ways to build linear models in R, but we will use buildModel, as mentioned above. First, we will use least squares regression to model the relationship between input and output variables. Suppose we want to know if the abundances of ADP and AMP are related in our metabolomics dataset:

ggplot(metabolomics_data) +
  geom_point(aes(x = ADP, y = AMP))
## Don't know how to automatically pick scale for object of
## type <impute>. Defaulting to continuous.

It looks like there might be a relationship! Let’s build an inferential model to examine the details of that that relationship:

basic_regression_model <- buildModel2(
  data = metabolomics_data,
  model_type = "linear_regression",
  input_variables = "ADP",
  output_variable = "AMP"
)
names(basic_regression_model)
## [1] "model_type" "model"      "metrics"

The output of buildModel consists of three things: the model_type, the model itself, and the metric describing certain aspects of the model and/or its performance. Let’s look at the model:

basic_regression_model$model
## 
## Call:
## lm(formula = formula, data = data, model = TRUE, x = TRUE, y = TRUE, 
##     qr = TRUE)
## 
## Coefficients:
## (Intercept)          ADP  
##      4.5764       0.6705

This is a linear model stored inside a special object type inside R called an lm. They can be a bit tricky to work with, but we have a way to make it easier - we’ll look at that in a second. Before that, let’s look at the metrics.

basic_regression_model$metrics
##               variable   value std_err        type  p_value
## 1            r_squared  0.4693      NA   statistic       NA
## 2    total_sum_squares 38.6346      NA   statistic       NA
## 3 residual_sum_squares 20.5024      NA   statistic       NA
## 4          (Intercept)  4.5764  0.9667 coefficient 8.04e-06
## 5                  ADP  0.6705  0.0747 coefficient 0.00e+00
##   p_value_adj
## 1          NA
## 2          NA
## 3          NA
## 4    8.04e-06
## 5    0.00e+00

It shows us the r-squared, the total and residual sum of squares, the intercept (b in y = mx + b), and the coefficient for AMP (i.e. the slope, m), as well some other things (we will talk about them in a second).

We can also use a function called predictWithModel to make some predictions using the model. Let’s try that for ADP and AMP. What we do is give it the model, and then tell it what values we want to predict for. In this case, we want to predict the abundance of ADP for each value of AMP in our data set. We can do that like this:

AMP_values_predicted_from_ADP_values <- predictWithModel(
  data = metabolomics_data,
  model_type = "linear_regression",
  model = basic_regression_model$model
)
head(AMP_values_predicted_from_ADP_values)
##        1        2        3        4        5        6 
## 13.18461 13.35352 13.48067 13.42760 12.57818 13.18366

So, predictWithModel is using the model to predict AMP values from ADP. However, note that we have the measured AMP values in our data set. We can compare the predicted values to the measured values to see how well our model is doing. We can do that like this:

ADP_values <- metabolomics_data$ADP

predictions_from_basic_linear_model <- data.frame(
    ADP_values = ADP_values,
    AMP_values_predicted_from_ADP_values = AMP_values_predicted_from_ADP_values,
    AMP_values_measured = metabolomics_data$AMP
)

plot1 <- ggplot() +
    geom_line(
        data = predictions_from_basic_linear_model,
        aes(x = ADP_values, y = AMP_values_predicted_from_ADP_values), color = "red"
    ) +
    geom_point(
        data = predictions_from_basic_linear_model,
        aes(x = ADP_values, y = AMP_values_predicted_from_ADP_values), color = "red"
    ) +
    geom_point(
        data = metabolomics_data,
        aes(x = ADP, y = AMP), color = "blue"
    )
plot1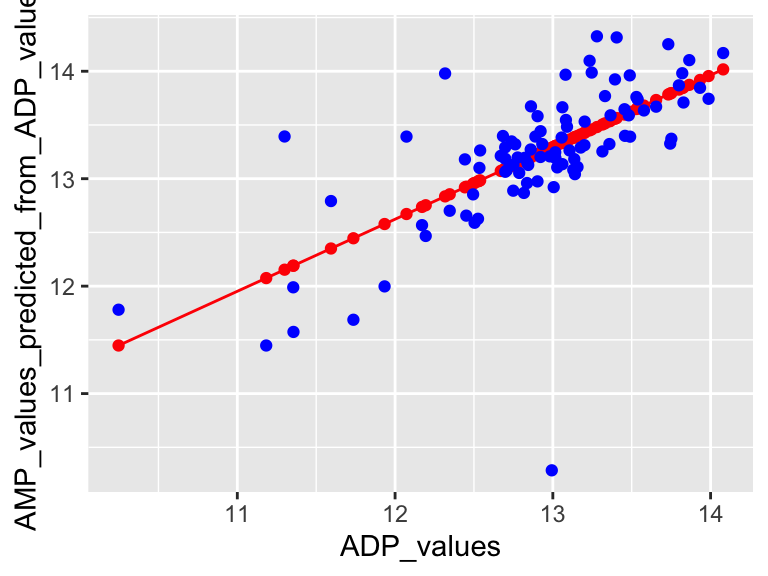
## Don't know how to automatically pick scale for object of
## type <impute>. Defaulting to continuous.

Very good. Now let’s talk about evaluating the quality of our model. For this we need some means of assessing how well our line fits our data. We will use residuals - the distance between each of our points and our line.

ggplot(predictions_from_basic_linear_model) +
  geom_point(aes(x = ADP_values, y = AMP_values_measured)) +
  geom_line(aes(x = ADP_values, y = AMP_values_predicted_from_ADP_values)) +
  geom_segment(aes(x = ADP_values, y = AMP_values_measured, xend = ADP_values, yend = AMP_values_predicted_from_ADP_values))
## Don't know how to automatically pick scale for object of
## type <impute>. Defaulting to continuous.

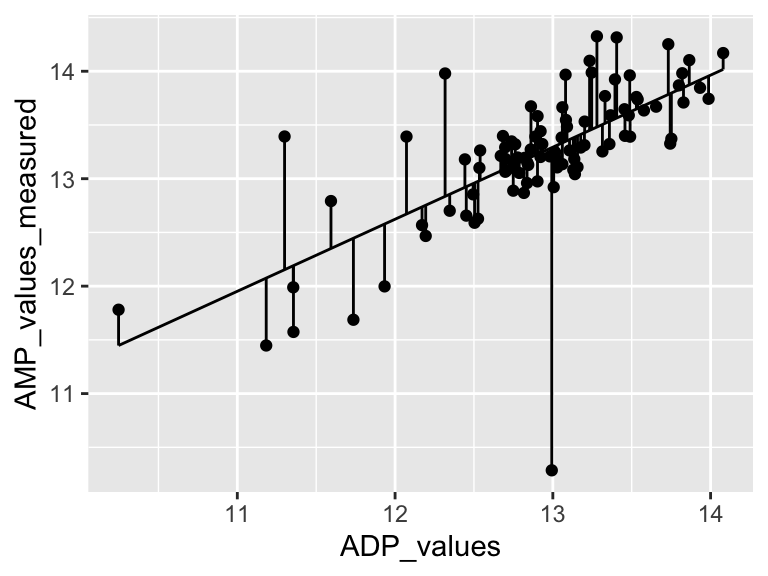
We can calculate the sum of the squared residuals:

sum(
  (predictions_from_basic_linear_model$AMP_values_measured - predictions_from_basic_linear_model$AMP_values_predicted_from_ADP_values)^2
, na.rm = TRUE)
## [1] 20.50235

Cool! Let’s call that the “residual sum of the squares”. So… does that mean our model is good? I don’t know. We have to compare that number to something. Let’s compare it to a super simple model that is just defined by the mean y value of the input data.

ggplot(metabolomics_data) +
  geom_point(aes(x = ADP, y = AMP)) +
  geom_hline(aes(yintercept = mean(AMP, na.rm = TRUE)))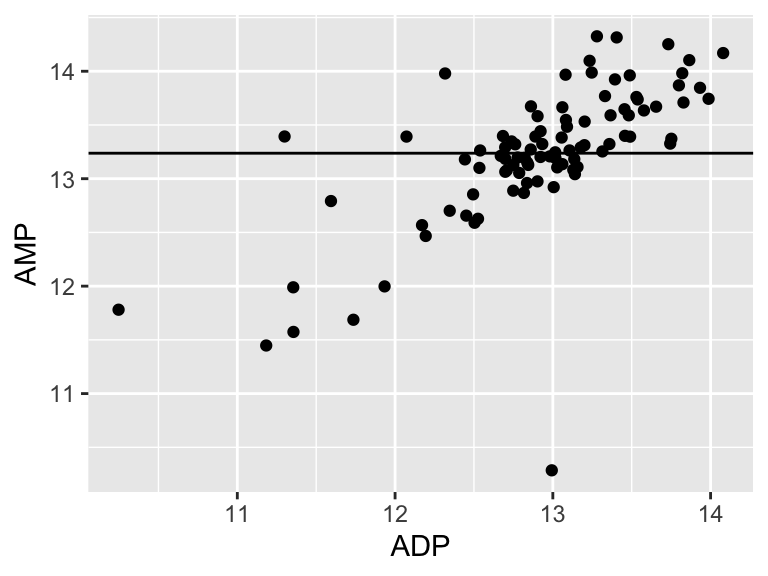
## Don't know how to automatically pick scale for object of
## type <impute>. Defaulting to continuous.

A pretty bad model, I agree. How much better is our linear model that the flat line model? Let’s create a measure of the distance between each point and the point predicted for that same x value on the model:

ggplot(metabolomics_data) +
  geom_point(aes(x = ADP, y = AMP)) +
  geom_hline(aes(yintercept = mean(ADP, na.rm = TRUE))) +
  geom_segment(aes(x = ADP, y = AMP, xend = ADP, yend = mean(ADP, na.rm = TRUE)))
## Don't know how to automatically pick scale for object of
## type <impute>. Defaulting to continuous.


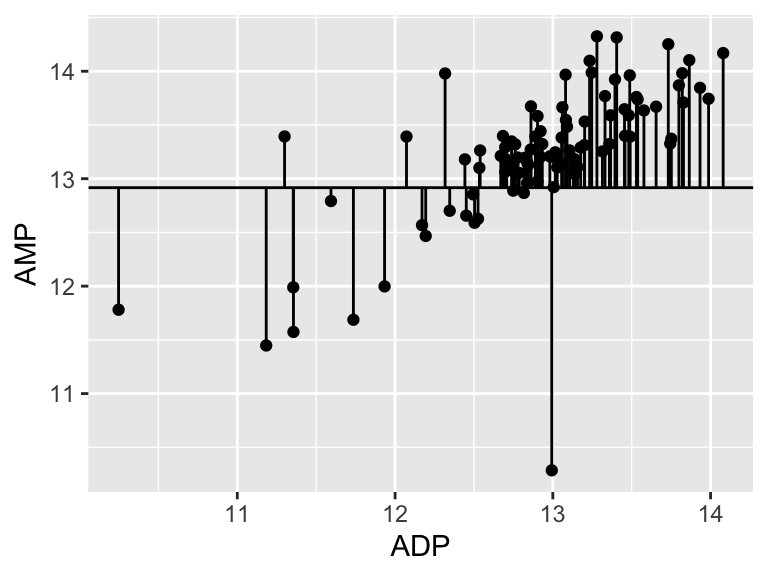
sum(
  (metabolomics_data$AMP - mean(metabolomics_data$AMP, na.rm = TRUE))^2
, na.rm = TRUE)
## [1] 38.63462

Cool. Let’s call that the “total sum of the squares”, and now we can compare that to our “residual sum of the squares”:

1-(20.1904/38.63)
## [1] 0.4773389

Alright. That is our R squared value. It is equal to 1 minus the ratio of the “residual sum of the squares” to the “total sum of the squares”. You can think of the R squared value as: - The amount of variance in the response explained by the dependent variable. - How much better the line of best fit describes the data than the flat line. Now, let’s put it all together and make it pretty:

top <- ggplot() +
    geom_line(
        data = predictions_from_basic_linear_model,
        aes(x = ADP_values, y = AMP_values_predicted_from_ADP_values), color = "red"
    ) +
    geom_point(
        data = predictions_from_basic_linear_model,
        aes(x = ADP_values, y = AMP_values_predicted_from_ADP_values), color = "red"
    ) +
    geom_point(
        data = metabolomics_data,
        aes(x = ADP, y = AMP), color = "blue"
    ) +
    annotate(geom = "table",
      x = 10,
      y = 15,
      label = list(select(basic_regression_model$metrics, variable, value))
    ) +
    coord_cartesian(ylim = c(10,16)) +
    theme_bw()

bottom <- ggplot(predictions_from_basic_linear_model) +
  geom_col(
    aes(x = ADP_values, y = AMP_values_measured-AMP_values_predicted_from_ADP_values),
    width = 0.03, color = "black", position = "dodge", alpha = 0.5
  ) +
  theme_bw()

cowplot::plot_grid(top, bottom, ncol = 1, labels = "AUTO", rel_heights = c(2,1))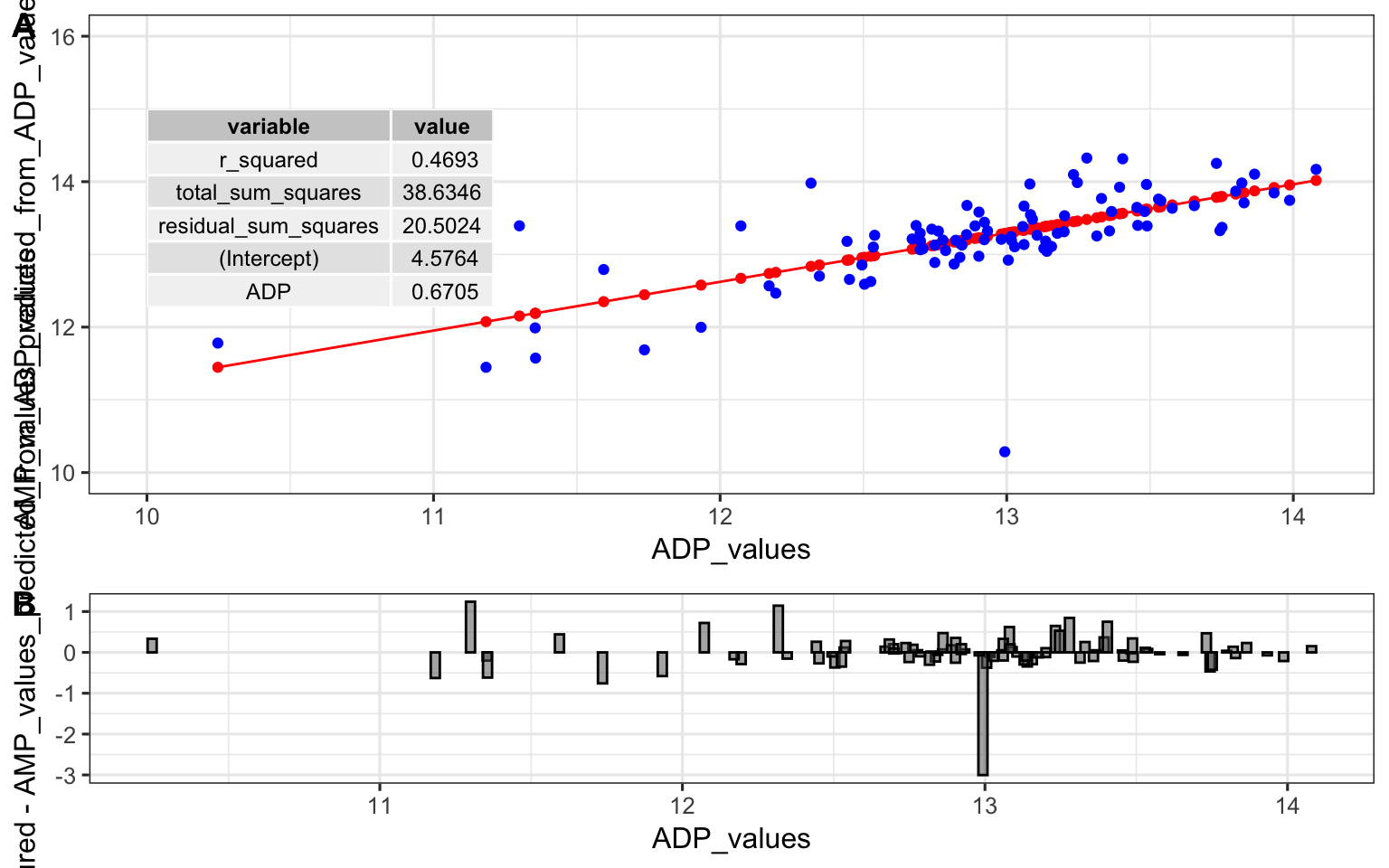
## Don't know how to automatically pick scale for object of
## type <impute>. Defaulting to continuous.
## Don't know how to automatically pick scale for object of
## type <impute>. Defaulting to continuous.

multiple linear regression

Cool! Now let’s try a multiple linear regression model. This is the same as a simple linear regression model, but with more than one predictor variable. Simple and multiple linear regression are both statistical methods used to explore the relationship between one or more independent variables (predictor variables) and a dependent variable (outcome variable). Simple linear regression involves one independent variable to predict the value of one dependent variable, utilizing a linear equation of the form y = mx + b. Multiple linear regression extends this concept to include two or more independent variables, with a typical form of y = m1x1 + m2x2 + … + b, allowing for a more complex representation of relationships among variables. While simple linear regression provides a straight-line relationship between the independent and dependent variables, multiple linear regression can model a multi-dimensional plane in the variable space, providing a more nuanced understanding of how the independent variables collectively influence the dependent variable. The complexity of multiple linear regression can offer more accurate predictions and insights, especially in scenarios where variables interact or are interdependent, although it also requires a more careful consideration of assumptions and potential multicollinearity among the independent variables. Let’s try it with the first 30 metabolites in our data set:


basic_regression_model <- buildModel2(
  data = metabolomics_data,
  model_type = "linear_regression",
  input_variables = "ADP",
  output_variable = "AMP"
)

multiple_regression_model <- buildModel2(
  data = metabolomics_data,
  model_type = "linear_regression",
  input_variables = colnames(metabolomics_data)[3:33],
  output_variable = "AMP"
)

ggplot() +
  geom_point(
    data = metabolomics_data,
    aes(x = ADP, y = AMP), fill = "gold", shape = 21, color = "black"
  ) +
  geom_line(aes(
    x = metabolomics_data$ADP,
    y = mean(metabolomics_data$AMP)
  ), color = "grey") +
  geom_line(aes(
    x = metabolomics_data$ADP,
    y = predictWithModel(
      data = metabolomics_data,
      model_type = "linear_regression",
      model = basic_regression_model$model
    )),
    color = "maroon", size = 1
  ) +
  geom_line(aes(
    x = metabolomics_data$ADP,
    y = predictWithModel(
      data = metabolomics_data,
      model_type = "linear_regression",
      model = multiple_regression_model$model
    )),
    color = "black", size = 1, alpha = 0.6
  ) +
  theme_bw()
## Don't know how to automatically pick scale for object of
## type <impute>. Defaulting to continuous.

assessing regression models

There are three aspects of a regression model that we should check on, to make sure the model isn’t violating and assumptions that we make when declaring the model to be valid:

Residual-Based Assumptions. These checks are specifically about the behavior of residuals, which are the differences between observed values and model predictions. This group includes:
- Linearity: Examines if residuals show a random scatter around zero, indicating a linear relationship between predictors and the response variable. Patterns or curves in this plot may indicate that the model does not adequately capture the true relationship, suggesting potential non-linearity.
- Homoscedasticity (Homogeneity of Variance): Looks at the spread of residuals to confirm that variance is consistent across fitted values. In other words, the spread of the residuals should be uniform regardless of the fitted values. To assess homoscedasticity, residuals are plotted against fitted values. A horizontal band of residuals indicates that the variance is consistent, supporting the homoscedasticity assumption. Conversely, patterns such as a funnel shape, where residuals spread out or contract as fitted values increase, suggest heteroscedasticity, indicating that the variance of errors changes with the level of the independent variables.
- Normality of Residuals: Assesses whether residuals follow a normal distribution, crucial for statistical inference in regression. To check this characteristic, a Quantile-Quantile (Q-Q) plot is used, where the residuals are plotted against a theoretical normal distribution. If the residuals are normally distributed, the points will align closely along a straight line. Significant deviations from this line indicate departures from normality, which may affect the reliability of statistical inferences drawn from the model.
Predictor Relationships: This check pertains to relationships among the predictor/input variables themselves, rather than their relationship with the response/output variable. In this case:
- Collinearity: Assesses multicollinearity, which occurs when predictors are highly correlated with each other. This can lead to inflated variances of regression coefficients, making it challenging to attribute effects to individual predictors. This check helps ensure that predictors are independent enough to provide clear, interpretable results for each variable’s influence on the response.
Model Fit and Influence: These checks look at the overall fit of the model and assess if specific data points have undue influence on the model’s results. This group includes:
- Posterior Predictive Check: This checks if model predictions align well with observed data, indicating a good overall fit. While not directly a residual analysis, it’s a comprehensive check for how well the model captures data patterns.
- Influential Observations: Identifies data points that might disproportionately affect the model. High-leverage points can distort model estimates, so it’s important to verify that no single observation is overly influential.

We can assess all of these using:

multiple_regression_model <- buildModel2(
  data = metabolomics_data,
  model_type = "linear_regression",
  input_variables = colnames(metabolomics_data)[3:10],
  output_variable = "AMP"
)

check_model(multiple_regression_model$model)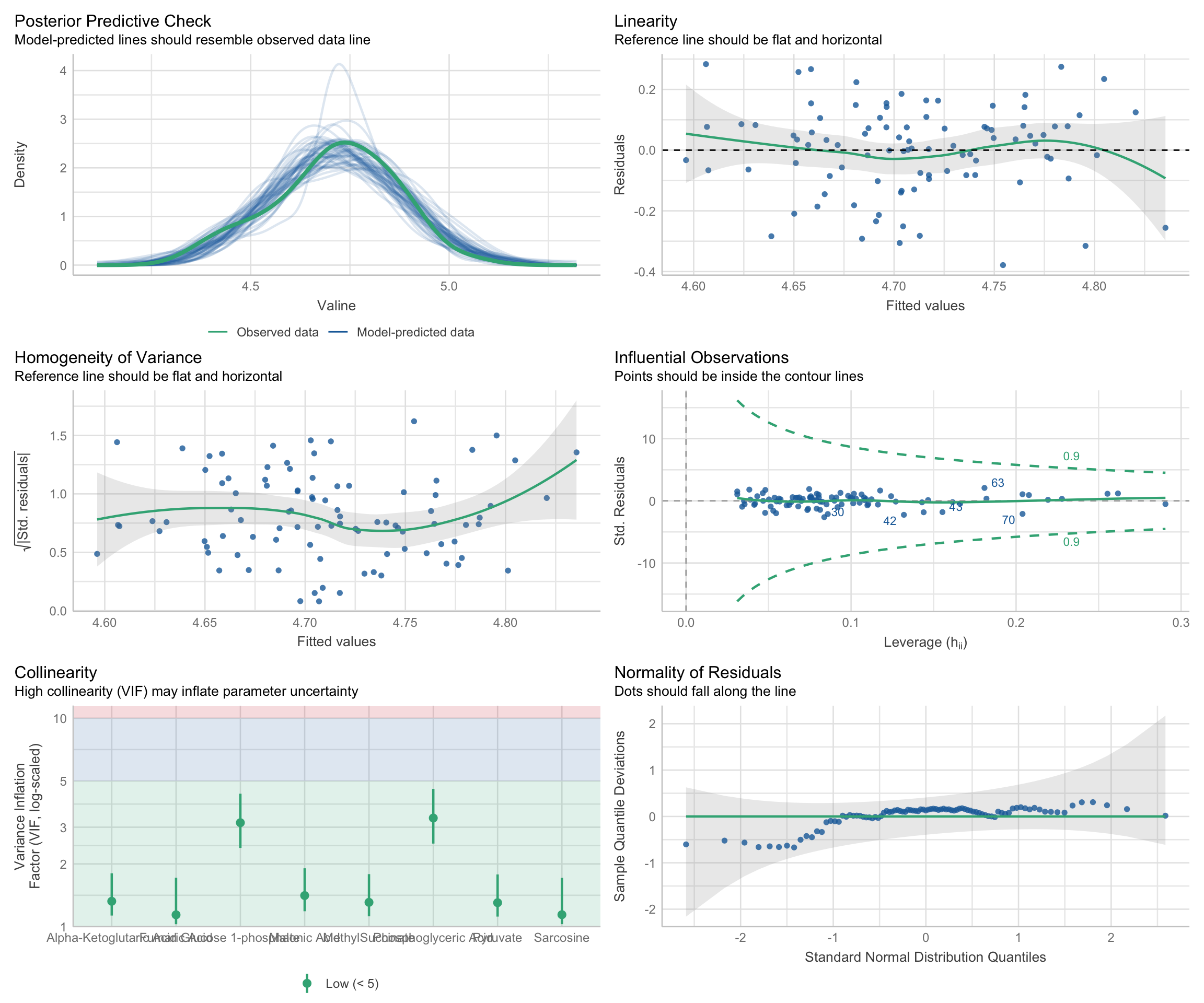

random forests

Random forests are collections of decision trees that can be used for predicting categorical variables (i.e. a ‘classification’ task) and for predicting numerical variables (a ‘regression’ task). Random forests are built by constructing multiple decision trees, each using a randomly selected subset of the training data, to ensure diversity among the trees. At each node of each tree, a number of input variables are randomly chosen as candidates for splitting the data, introducing further randomness beyond the data sampling. Among the variables randomly selected as candidates for splitting at each node, one is chosen for that node based on a criterion, such as maximizing purity in the tree’s output, or minimizing mean squared error for regression tasks, guiding the construction of a robust ensemble model. The forest’s final prediction is derived either through averaging the outputs (for regression) or a majority vote (for classification).

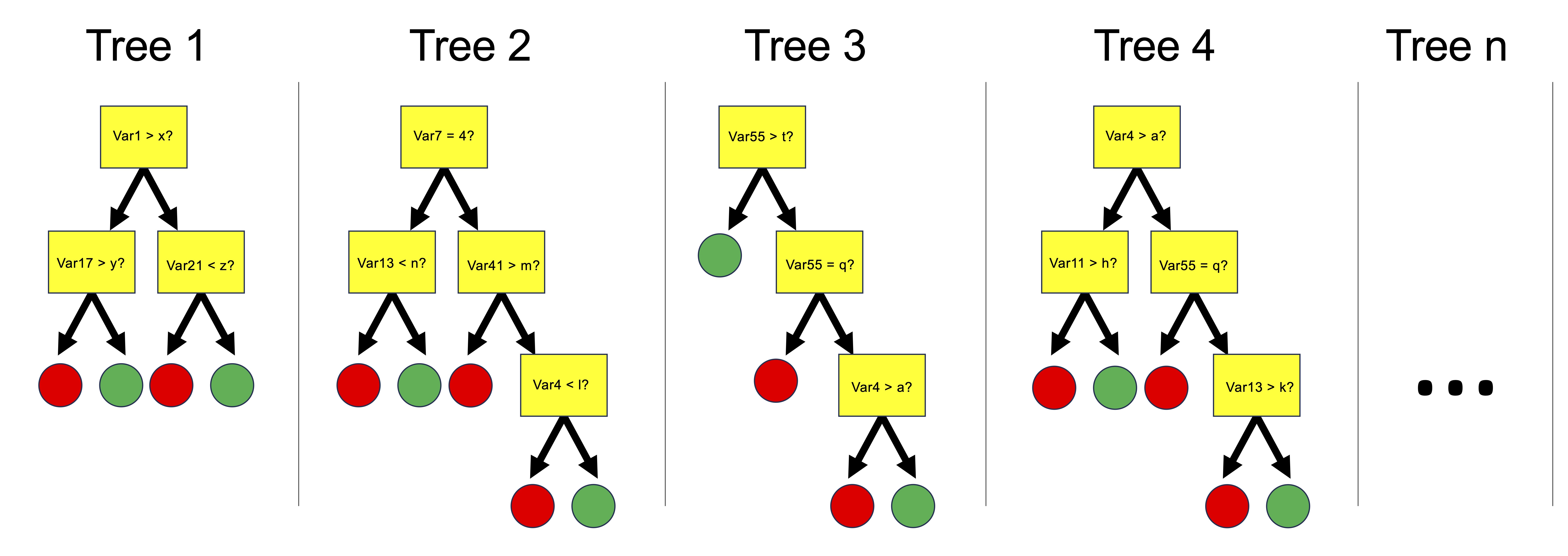
We can use the buildModel() function to make a random forest model. We need to specify data, a model type, input and output variables, and in the case of a random forest model, we also need to provide a list of optimization parameters: n_vars_tried_at_split, n_trees, and min_n_leaves. Here is more information on those parameters:

n_vars_at_split (often called “mtry” in other implementations): this parameter specifies the number of variables that are randomly sampled as candidate features at each split point in the construction of a tree. The main idea behind selecting a subset of features (variables) is to introduce randomness into the model, which helps in making the model more robust and less likely to overfit to the training data. By trying out different numbers of features, the model can find the right level of complexity, leading to more generalized predictions. A smaller value of n_vars_at_split increases the randomness of the forest, potentially increasing bias but decreasing variance. Conversely, a larger mtry value makes the model resemble a bagged ensemble of decision trees, potentially reducing bias but increasing variance.
n_trees (often referred to as “num.trees” or “n_estimators” in other implementations): this parameter defines the number of trees that will be grown in the random forest. Each individual tree predicts the outcome based on the subset of features it considers, and the final prediction is typically the mode (for classification tasks) or average (for regression tasks) of all individual tree predictions. Increasing the number of trees generally improves the model’s performance because it averages more predictions, which tends to reduce overfitting and makes the model more stable. However, beyond a certain point, adding more trees offers diminishing returns in terms of performance improvement and can significantly increase computational cost and memory usage without substantial gains.
min_n_leaves (often referred to as “min_n” in other implementations, default value is 1): This parameter sets the minimum number of samples that must be present in a node for it to be split further. Increasing this value makes each tree in the random forest less complex by reducing the depth of the trees, leading to larger, more generalized leaf nodes. This can help prevent overfitting by ensuring that the trees do not grow too deep or too specific to the training data. By carefully tuning this parameter, you can strike a balance between the model’s ability to capture the underlying patterns in the data and its generalization to unseen data.

buildModel() is configured to allow you to explore a number of settings for both n_vars_at_split and n_trees, then pick the combination with the highest predictive accuracy. In this function:

data specifies the dataset to be used for model training, here metabolomics_data.
model_type defines the type of model to build, with “random_forest_regression” indicating a random forest model for regression tasks.
input_variables selects the features or predictors for the model, here using columns 3 to 33 from metabolomics_data as predictors.
output_variable is the target variable for prediction, in this case, “AMP”.

The optimization_parameters argument takes a list to define the grid of parameters for optimization, including n_vars_tried_at_split, n_trees, and min_leaf_size. The seq() function generates sequences of numbers and is used here to create ranges for each parameter:

n_vars_tried_at_split = seq(1,24,3) generates a sequence for the number of variables tried at each split, starting at 1, ending at 24, in steps of 3 (e.g., 1, 4, 7, …, 24).
n_trees = seq(1,40,2) creates a sequence for the number of trees in the forest, from 1 to 40 in steps of 2.
min_leaf_size = seq(1,3,1) defines the minimal size of leaf nodes, ranging from 1 to 3 in steps of 1.

This setup creates a grid of parameter combinations where each combination of n_vars_tried_at_split, n_trees, and min_leaf_size defines a unique random forest model. The function will test each combination within this grid to identify the model that performs best according to a given evaluation criterion, effectively searching through a defined parameter space to optimize the random forest’s performance. This approach allows for a systematic exploration of how different configurations affect the model’s ability to predict the output variable, enabling the selection of the most effective model configuration based on the dataset and task at hand.

random_forest_model <- buildModel2(
    data = metabolomics_data,
    model_type = "random_forest_regression",
    input_variables = colnames(metabolomics_data)[3:33],
    output_variable = "AMP",
    optimization_parameters = list(
      n_vars_tried_at_split = seq(1,24,3),
      n_trees = seq(1,40,2),
      min_leaf_size = seq(1,3,1)
    )
)

names(random_forest_model)
## [1] "metrics" "model"

The above code builds our random forest model. It’s output provides both the model itself and key components indicating the performance and configuration of the model. Here’s a breakdown of each part of the output:

$model_type tells us what type of model this is.

$model shows the configuration of the best random forest model that was created.

$metrics provides detailed results of model performance across different combinations of the random forest parameters n_vars_tried_at_split (the number of variables randomly sampled as candidates at each split) and n_trees (the number of trees in the forest). For each combination, it shows: - n_vars_tried_at_split and n_trees: The specific values used in that model configuration. - .metric: The performance metric used, here it’s accuracy, which measures how often the model correctly predicts the patient status. - .estimator: Indicates the type of averaging used for the metric, here it’s binary for binary classification tasks. - mean: The average accuracy across the cross-validation folds. - fold_cross_validation: Indicates the number of folds used in cross-validation, here it’s 3 for all models. - std_err: The standard error of the mean accuracy, providing an idea of the variability in model performance. - .config: A unique identifier for each model configuration tested.

We can thus inspect the performance of the model based on the specific parameters used during configuration. This can help us understand if we are exploring the right parameter space - do we have good values for n_vars_tried_at_split and n_trees? In this case we are doing regression, and the performance metric reported is RMSE: root mean squared error. We want that value to be small! So smaller values for that metric indicate a better model.

random_forest_model$metrics %>%
    ggplot(aes(x = mtry, y = trees, fill = mean)) +
    facet_grid(.~min_n) +
    scale_fill_viridis(direction = -1) +
    geom_tile() +
    theme_bw()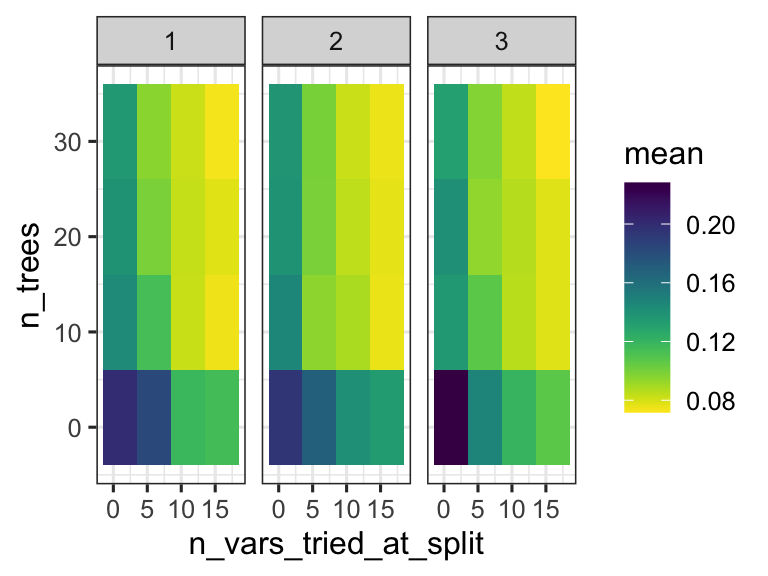

We can easily use the model to make predictions by using the predictWithModel() function:

ggplot() +
  geom_point(
    data = metabolomics_data,
    aes(x = ADP, y = AMP), fill = "gold", shape = 21, color = "black"
  ) +
  geom_line(aes(
    x = metabolomics_data$ADP,
    y = mean(metabolomics_data$AMP)
  ), color = "grey") +
  geom_line(aes(
    x = metabolomics_data$ADP,
    y = predictWithModel(
      data = metabolomics_data,
      model_type = "random_forest_regression",
      model = random_forest_model$model
    )),
    color = "maroon", size = 1
  ) +
  theme_bw()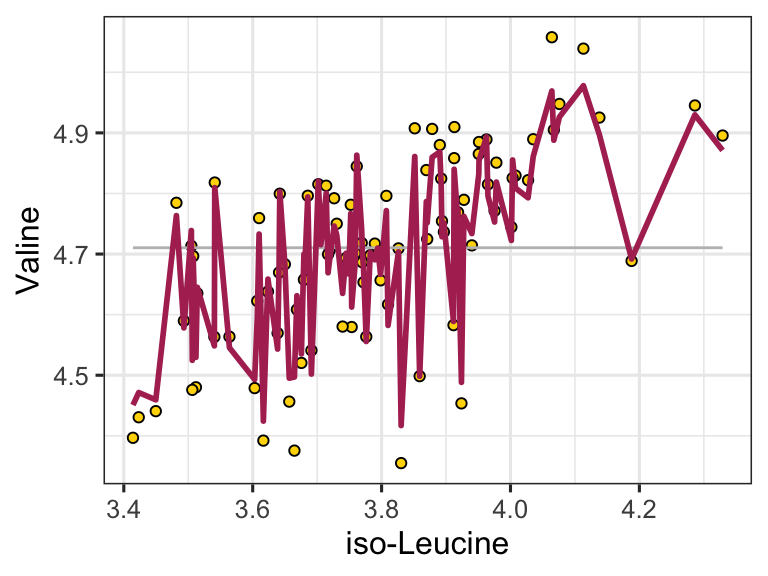
## Don't know how to automatically pick scale for object of
## type <impute>. Defaulting to continuous.

In addition to regression modeling, random forests can also be used to do classification modeling. In classification modeling, we are trying to predict a categorical outcome variable from a set of predictor variables. For example, we might want to predict whether a patient has a disease or not based on their metabolomics data. All we have to do is set the model_type to “random_forest_classification” instead of “random_forest_regression”. Let’s try that now:

set.seed(123)
unknown <- metabolomics_data[35:40,]

rfc <- buildModel2(
  data = metabolomics_data[c(1:34, 41:93),],
  model_type = "random_forest_classification",
  input_variables = colnames(metabolomics_data)[3:126],
  output_variable = "patient_status",
  optimization_parameters = list(
    n_vars_tried_at_split = seq(5,50,5),
    n_trees = seq(10,100,10),
    min_leaf_size = seq(1,3,1)
  )
)
rfc$metrics %>% arrange(desc(mean))
## # A tibble: 300 × 9
##    n_vars_tried_at_split n_trees min_n .metric  .estimator
##                    <dbl>   <dbl> <dbl> <chr>    <chr>     
##  1                    40      10     1 accuracy binary    
##  2                    40      60     3 accuracy binary    
##  3                    50      50     2 accuracy binary    
##  4                    40      20     2 accuracy binary    
##  5                    30     100     1 accuracy binary    
##  6                    35      50     2 accuracy binary    
##  7                    15      20     3 accuracy binary    
##  8                    50     100     3 accuracy binary    
##  9                    25      10     1 accuracy binary    
## 10                    30      20     1 accuracy binary    
## # ℹ 290 more rows
## # ℹ 4 more variables: mean <dbl>,
## #   fold_cross_validation <int>, std_err <dbl>,
## #   .config <chr>

Cool! Our best settings lead to a model with 90% accuracy! We can also make predictions on unknown data with this model:

rfc$metrics %>%
    ggplot(aes(x = n_vars_tried_at_split, y = n_trees, fill = mean)) +
    facet_grid(.~min_n) +
    scale_fill_viridis(direction = -1) +
    geom_tile() +
    theme_bw()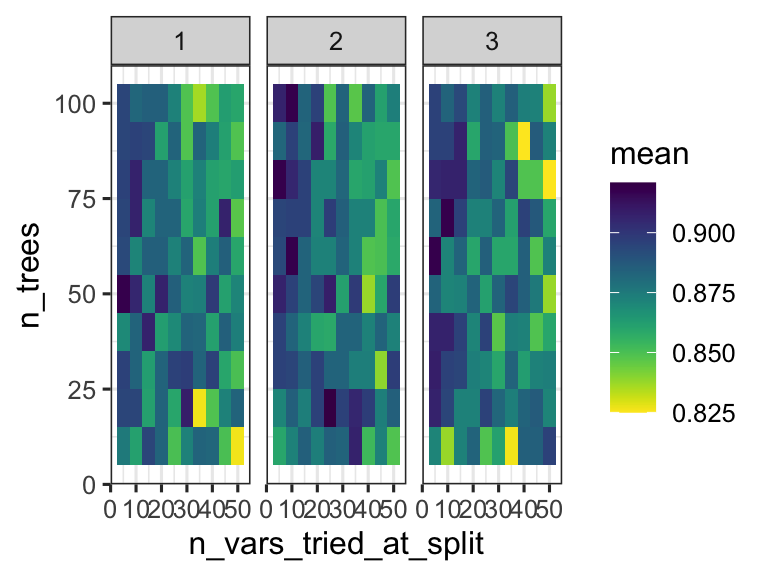

predictions <- predictWithModel(
  data = unknown,
  model_type = "random_forest_classification",
  model = rfc$model
)

data.frame(
  real_status = metabolomics_data[35:40,]$patient_status,
  predicted_status = predictions
)
##                 real_status predicted_status
## .pred_class1        healthy          healthy
## .pred_class2        healthy          healthy
## .pred_class3        healthy          healthy
## .pred_class4 kidney_disease   kidney_disease
## .pred_class5 kidney_disease   kidney_disease
## .pred_class6 kidney_disease   kidney_disease

exercises

To practice creating models, try the following:

Choose one of the datasets we have used so far, and run a principal components analysis on it. Note that the output of the analysis when you run “pca” contains the Dimension 1 coordinate “Dim.1” for each sample, as well as the abundance of each analyte in that sample.
Using the information from the ordination plot, identify two analytes: one that has a variance that is strongly and positively correlated with the first principal component (i.e. dimension 1), and one that has a variance that is slightly less strongly, but still positively correlated with the first principal component. Using buildModel, create and plot two linear regression models, one that regresses each of those analytes against dimension 1 (in other words, the x-axis should be the Dim.1 coordinate for each sample, and the y-axis should be the values for one of the two selected analytes). Which has the greater r-squared value? Based on what you know about PCA, does that make sense?
Choose two analytes: one should be one of the analytes from question 2 above, the other should be an analyte that, according to your PCA ordination analysis, is negatively correlated with the first principal component. Using buildModel and predictWithModel create plots showing how those two analytes are correlated with dimension 1. One should be positively correlated, and the other negatively correlated.
Have a look at the dataset metabolomics_unknown. It is metabolomics data from patients with an unknown healthy/kidney disease status. Build a classification model using the metabolomics_data dataset and diagnose each patient in metabolomics_unknown.
(optional) Explore the wine_quality dataset. What are the most important factors in determining what is a good wine? Use a model in an inferential way to provide evidence for your answer.

comparing means

embedding models

Integrated Bioanalytics