dimensionality reduction

In the previous chapters, we looked at how to explore our data sets by visualizing many variables and manually identifying trends. Sometimes, we encounter data sets with so many variables, that it is not reasonable to manually select certain variables with which to create plots and manually search for trends. In these cases, we need dimensionality reduction - a set of techniques that helps us identify which variables are driving differences among our samples. In this course, we will conduct dimensionality reduction useing runMatrixAnalysis(), a function that is loaded into your R Session when you run the source() command.
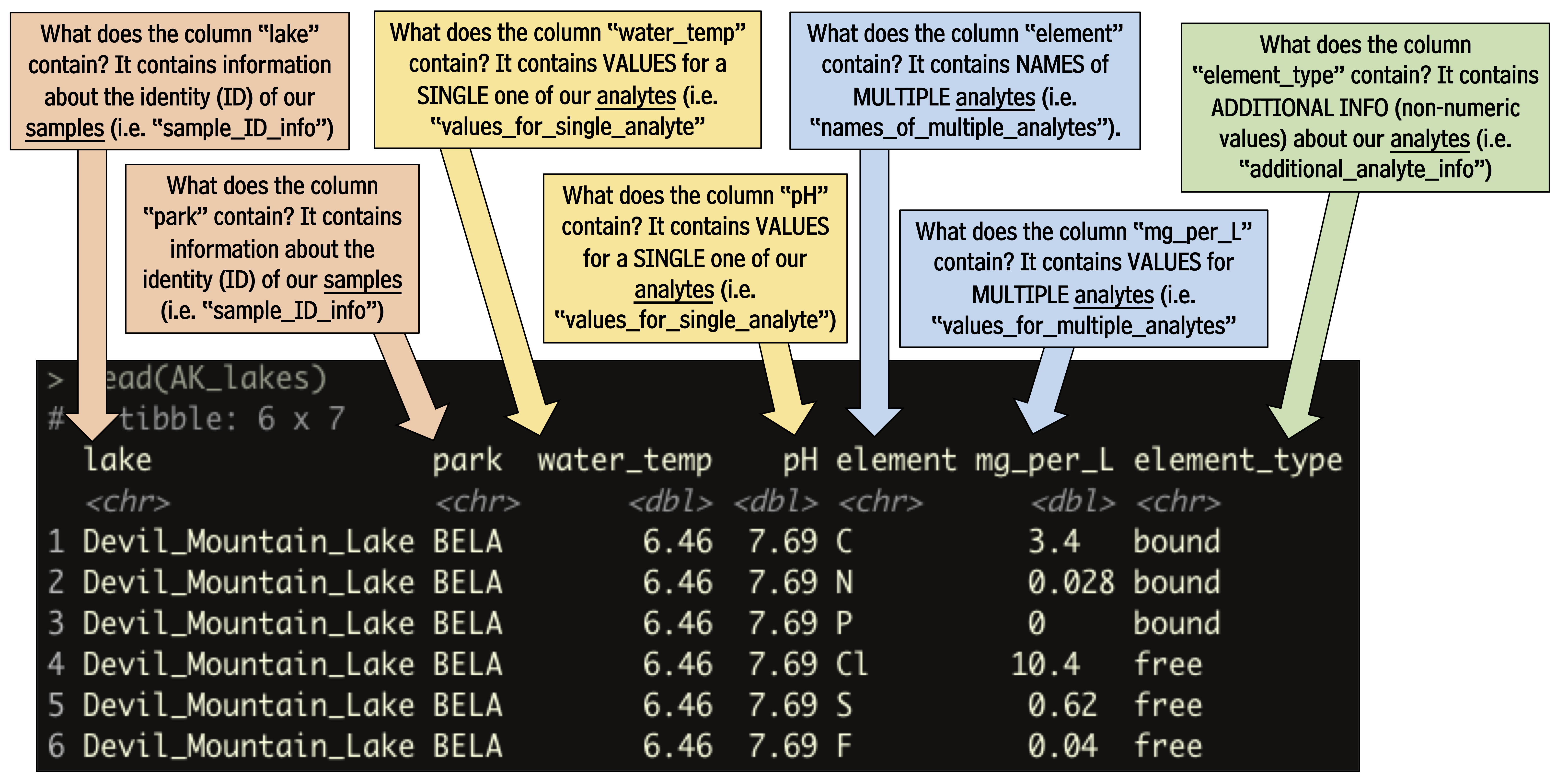
Matrix analyses can be a bit tricky to set up. There are two things that we can do to help us with this: (i) we will use a template for runMatrixAnalysis() (see below) and (ii) it is critical that we think about our data in terms of samples and analytes. Let’s consider our Alaska lakes data set:
alaska_lake_data
## # A tibble: 220 × 7
## lake park water_temp pH element mg_per_L
## <chr> <chr> <dbl> <dbl> <chr> <dbl>
## 1 Devil_Mountain_L… BELA 6.46 7.69 C 3.4
## 2 Devil_Mountain_L… BELA 6.46 7.69 N 0.028
## 3 Devil_Mountain_L… BELA 6.46 7.69 P 0
## 4 Devil_Mountain_L… BELA 6.46 7.69 Cl 10.4
## 5 Devil_Mountain_L… BELA 6.46 7.69 S 0.62
## 6 Devil_Mountain_L… BELA 6.46 7.69 F 0.04
## 7 Devil_Mountain_L… BELA 6.46 7.69 Br 0.02
## 8 Devil_Mountain_L… BELA 6.46 7.69 Na 8.92
## 9 Devil_Mountain_L… BELA 6.46 7.69 K 1.2
## 10 Devil_Mountain_L… BELA 6.46 7.69 Ca 5.73
## # ℹ 210 more rows
## # ℹ 1 more variable: element_type <chr>We can see that this dataset is comprised of measurements of various analytes (i.e. several chemical elements, as well as water_temp, and pH), in different samples (i.e. lakes). We need to tell the runMatrixAnalysis() function how each column relates to this samples and analytes structure. See the image below for an explanation.
pca
“Which analytes are driving differences among my samples?” “Which analytes in my data set are correlated?”
theory
PCA looks at all the variance in a high dimensional data set and chooses new axes within that data set that align with the directions containing highest variance. These new axes are called principal components. Let’s look at an example:
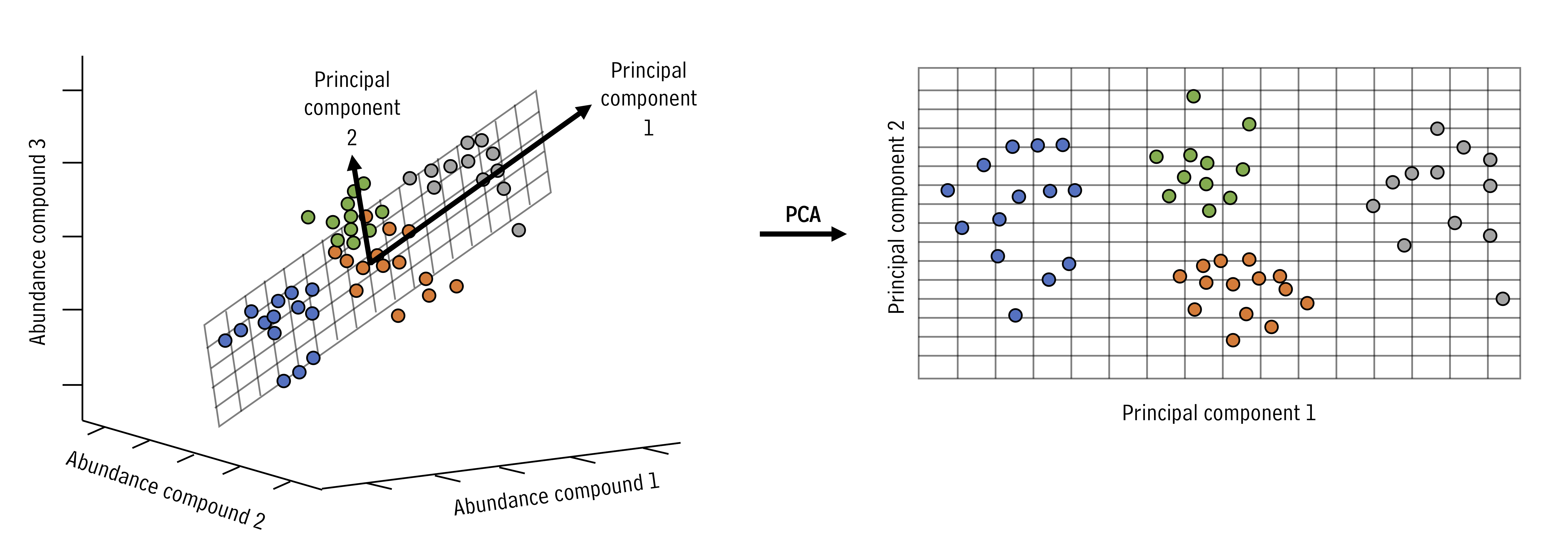
In the example above, the three dimensional space can be reduced to a two dimensional space with the principal components analysis. New axes (principal components) are selected (bold arrows on left) that become the x and y axes in the principal components space (right).
We can run and visualize principal components analyses using the runMatrixAnalysis() function as in the example below. As you can see in the output, the command provides the sample_IDs, sample information, then the coordinates for each sample in the 2D projection (the “PCA plot”) and the raw data, in case you wish to do further processing.
AK_lakes_pca <- runMatrixAnalysis(
data = alaska_lake_data,
analysis = c("pca"),
column_w_names_of_multiple_analytes = "element",
column_w_values_for_multiple_analytes = "mg_per_L",
columns_w_values_for_single_analyte = c("water_temp", "pH"),
columns_w_additional_analyte_info = "element_type",
columns_w_sample_ID_info = c("lake", "park"),
scale_variance = TRUE
)
## Replacing NAs in your data with mean
head(AK_lakes_pca)
## # A tibble: 6 × 18
## sample_unique_ID lake park Dim.1 Dim.2 water_temp
## <chr> <chr> <chr> <dbl> <dbl> <dbl>
## 1 Devil_Mountain_Lake_… Devi… BELA 0.229 -0.861 6.46
## 2 Imuruk_Lake_BELA Imur… BELA -1.17 -1.62 17.4
## 3 Kuzitrin_Lake_BELA Kuzi… BELA -0.918 -1.15 8.06
## 4 Lava_Lake_BELA Lava… BELA 0.219 -1.60 20.2
## 5 North_Killeak_Lake_B… Nort… BELA 9.46 0.450 11.3
## 6 White_Fish_Lake_BELA Whit… BELA 4.17 -0.972 12.0
## # ℹ 12 more variables: pH <dbl>, C <dbl>, N <dbl>, P <dbl>,
## # Cl <dbl>, S <dbl>, F <dbl>, Br <dbl>, Na <dbl>,
## # K <dbl>, Ca <dbl>, Mg <dbl>Let’s plot the 2D projection of the Alaska lakes data:
ggplot(data = AK_lakes_pca, aes(x = Dim.1, y = Dim.2)) +
geom_point(aes(fill = park), shape = 21, size = 4, alpha = 0.8) +
geom_label_repel(aes(label = lake), alpha = 0.5) +
theme_classic()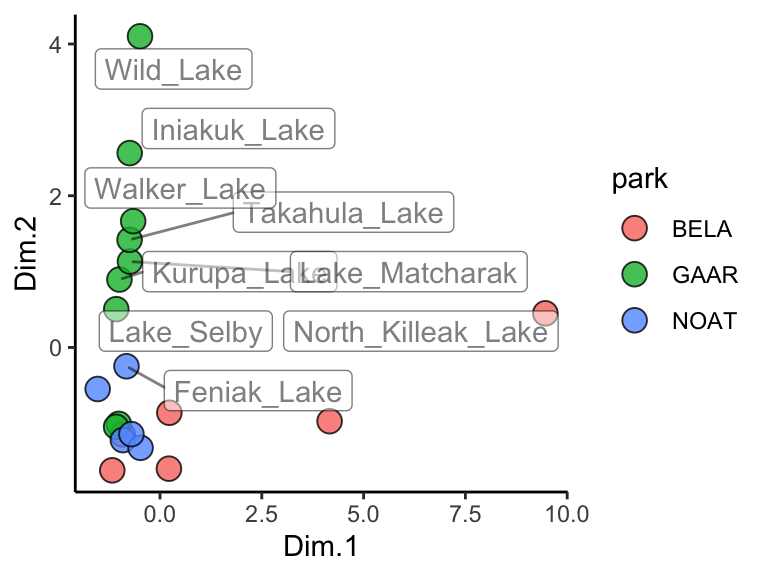
Great! In this plot we can see that White Fish Lake and North Killeak Lake, both in BELA park, are quite different from the other parks (they are separated from the others along dimension 1, i.e. the first principal component). At the same time, Wild Lake, Iniakuk Lake, Walker Lake, and several other lakes in GAAR park are different from all the others (they are separated from the others along dimension 2, i.e. the second principal component).
Important question: what makes the lakes listed above different from the others? Certainly some aspect of their chemistry, since that’s the data that this analysis is built upon, but how do we determine which analyte(s) are driving the differences among the lakes that we see in the PCA plot?
ordination plots
Let’s look at how to access the information about which analytes are major contributors to each principal component. This is important because it will tell you which analytes are associated with particular dimensions, and by extension, which analytes are associated with (and are markers for) particular groups in the PCA plot. This can be determined using an ordination plot. Let’s look at an example. We can obtain the ordination plot information using runMatrixAnalysis() with analysis = "pca_ord":
## Replacing NAs in your data with mean
## # A tibble: 6 × 3
## analyte Dim.1 Dim.2
## <chr> <dbl> <dbl>
## 1 water_temp 0.0750 -0.261
## 2 pH 0.686 0.0185
## 3 C 0.290 -0.242
## 4 N 0.00435 0.714
## 5 P 0.473 -0.0796
## 6 Cl 0.953 0.0148We can now visualize the ordination plot using our standard ggplot plotting techniques. Note the use of geom_label_repel() and filter() to label certain segments in the ordination plot. You do not need to use geom_label_repel(), you could use the built in geom_label(), but geom_label_repel() can make labelling your segments easier.
AK_lakes_pca_ord <- runMatrixAnalysis(
data = alaska_lake_data,
analysis = c("pca_ord"),
column_w_names_of_multiple_analytes = "element",
column_w_values_for_multiple_analytes = "mg_per_L",
columns_w_values_for_single_analyte = c("water_temp", "pH"),
columns_w_additional_analyte_info = "element_type",
columns_w_sample_ID_info = c("lake", "park")
)
## Replacing NAs in your data with mean
head(AK_lakes_pca_ord)
## # A tibble: 6 × 3
## analyte Dim.1 Dim.2
## <chr> <dbl> <dbl>
## 1 water_temp 0.0750 -0.261
## 2 pH 0.686 0.0185
## 3 C 0.290 -0.242
## 4 N 0.00435 0.714
## 5 P 0.473 -0.0796
## 6 Cl 0.953 0.0148
ggplot(AK_lakes_pca_ord) +
geom_segment(aes(x = 0, y = 0, xend = Dim.1, yend = Dim.2, color = analyte), size = 1) +
geom_circle(aes(x0 = 0, y0 = 0, r = 1)) +
geom_label_repel(
data = filter(AK_lakes_pca_ord, Dim.1 > 0.9, Dim.2 < 0.1, Dim.2 > -0.1),
aes(x = Dim.1, y = Dim.2, label = analyte), xlim = c(1,1.5)
) +
geom_label_repel(
data = filter(AK_lakes_pca_ord, Dim.2 > 0.5),
aes(x = Dim.1, y = Dim.2, label = analyte), direction = "y", ylim = c(1,1.5)
) +
coord_cartesian(xlim = c(-1,1.5), ylim = c(-1,1.5)) +
theme_bw()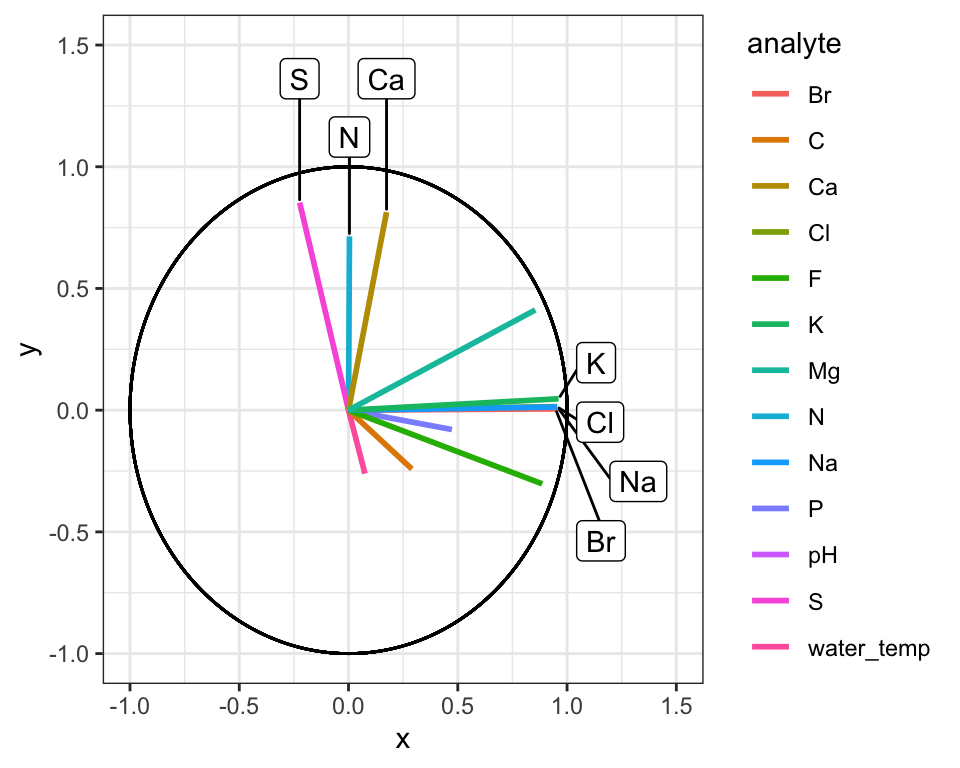
Great! Here is how to read the ordination plot:
When considering one analyte’s vector: the vector’s projected value on an axis shows how much its variance is aligned with that principal component.
When considering two analyte vectors: the angle between two vectors indicates how correlated those two variables are. If they point in the same direction, they are highly correlated. If they meet each other at 90 degrees, they are not very correlated. If they meet at ~180 degrees, they are negatively correlated. If say that one analyte is “1.9” with respect to dimension 2 and another is “-1.9” with respect to dimension 2. Let’s also say that these vectors are ~“0” with respect to dimension 1.
With the ordination plot above, we can now see that the abundances of K, Cl, Br, and Na are the major contributors of variance to the first principal component (or the first dimension). The abundances of these elements are what make White Fish Lake and North Killeak Lake different from the other lakes. We can also see that the abundances of N, S, and Ca are the major contributors to variance in the second dimension, which means that these elements ar what set Wild Lake, Iniakuk Lake, Walker Lake, and several other lakes in GAAR park apart from the rest of the lakes in the data set. It slightly easier to understand this if we look at an overlay of the two plots, which is often called a “biplot”:
AK_lakes_pca <- runMatrixAnalysis(
data = alaska_lake_data,
analysis = c("pca"),
column_w_names_of_multiple_analytes = "element",
column_w_values_for_multiple_analytes = "mg_per_L",
columns_w_values_for_single_analyte = c("water_temp", "pH"),
columns_w_additional_analyte_info = "element_type",
columns_w_sample_ID_info = c("lake", "park"),
scale_variance = TRUE
)
## Replacing NAs in your data with mean
AK_lakes_pca_ord <- runMatrixAnalysis(
data = alaska_lake_data,
analysis = c("pca_ord"),
column_w_names_of_multiple_analytes = "element",
column_w_values_for_multiple_analytes = "mg_per_L",
columns_w_values_for_single_analyte = c("water_temp", "pH"),
columns_w_additional_analyte_info = "element_type",
columns_w_sample_ID_info = c("lake", "park")
)
## Replacing NAs in your data with mean
ggplot() +
geom_point(
data = AK_lakes_pca,
aes(x = Dim.1, y = Dim.2, fill = park), shape = 21, size = 4, alpha = 0.8
) +
# geom_label_repel(aes(label = lake), alpha = 0.5) +
geom_segment(
data = AK_lakes_pca_ord,
aes(x = 0, y = 0, xend = Dim.1, yend = Dim.2, color = analyte),
size = 1
) +
scale_color_manual(values = discrete_palette) +
theme_classic()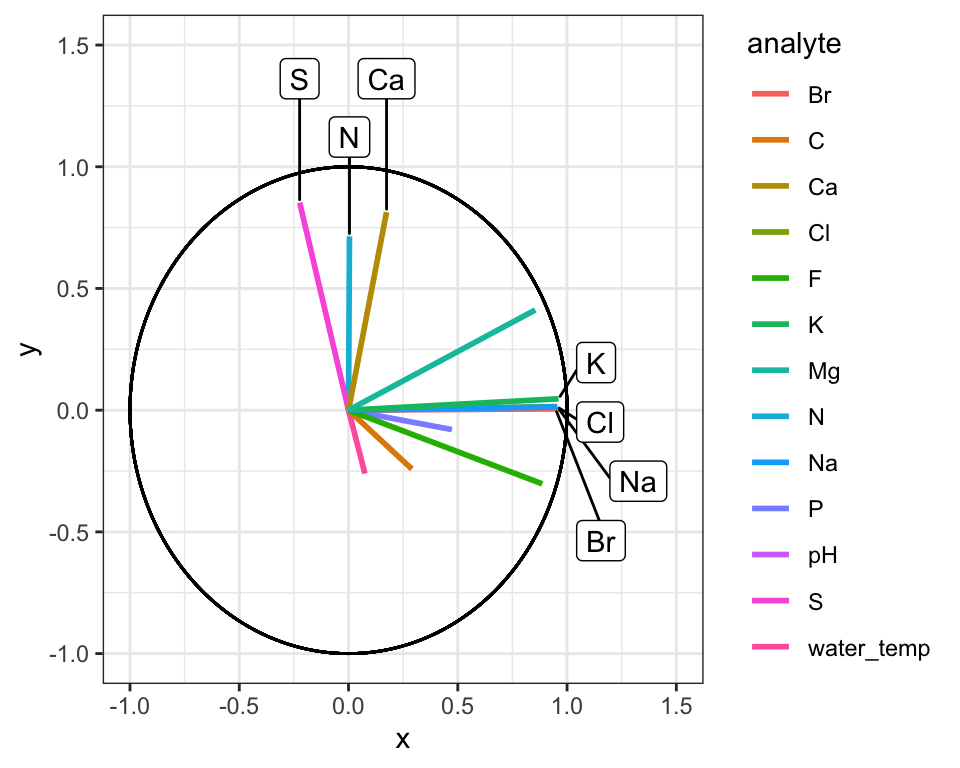
Note that you do not have to plot ordination data as a circular layout of segments. Sometimes it is much easier to plot (and interpret!) alternatives:
AK_lakes_pca_ord %>%
ggplot(aes(x = Dim.1, y = analyte)) +
geom_point(aes(fill = analyte), shape = 22, size = 3) +
scale_fill_manual(values = discrete_palette) +
theme_bw()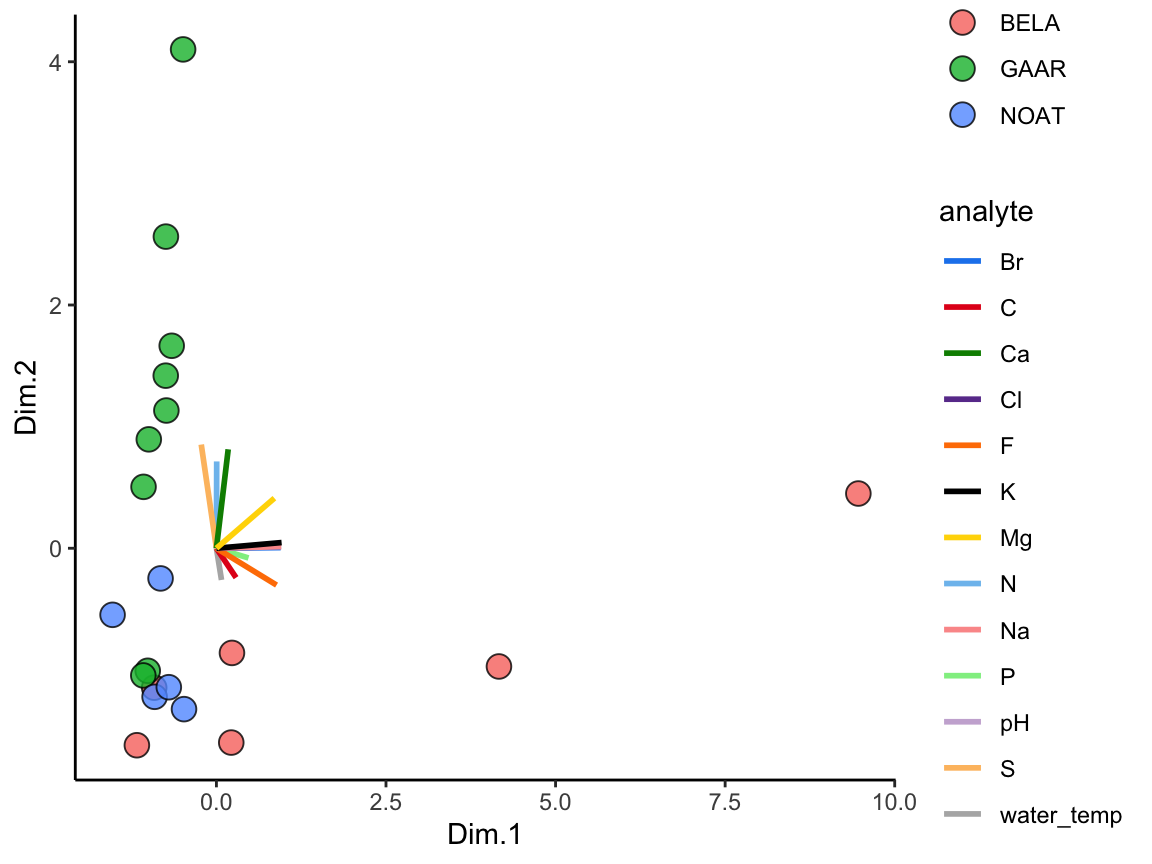
principal components
We also can access information about the how much of the variance in the data set is explained by each principal component, and we can plot that using ggplot:
AK_lakes_pca_dim <- runMatrixAnalysis(
data = alaska_lake_data,
analysis = c("pca_dim"),
column_w_names_of_multiple_analytes = "element",
column_w_values_for_multiple_analytes = "mg_per_L",
columns_w_values_for_single_analyte = c("water_temp", "pH"),
columns_w_additional_analyte_info = "element_type",
columns_w_sample_ID_info = c("lake", "park")
)
## Replacing NAs in your data with mean
head(AK_lakes_pca_dim)
## # A tibble: 6 × 2
## principal_component percent_variance_explained
## <dbl> <dbl>
## 1 1 48.8
## 2 2 18.6
## 3 3 11.6
## 4 4 7.88
## 5 5 4.68
## 6 6 3.33
ggplot(
data = AK_lakes_pca_dim,
aes(x = principal_component, y = percent_variance_explained)
) +
geom_line() +
geom_point() +
theme_bw()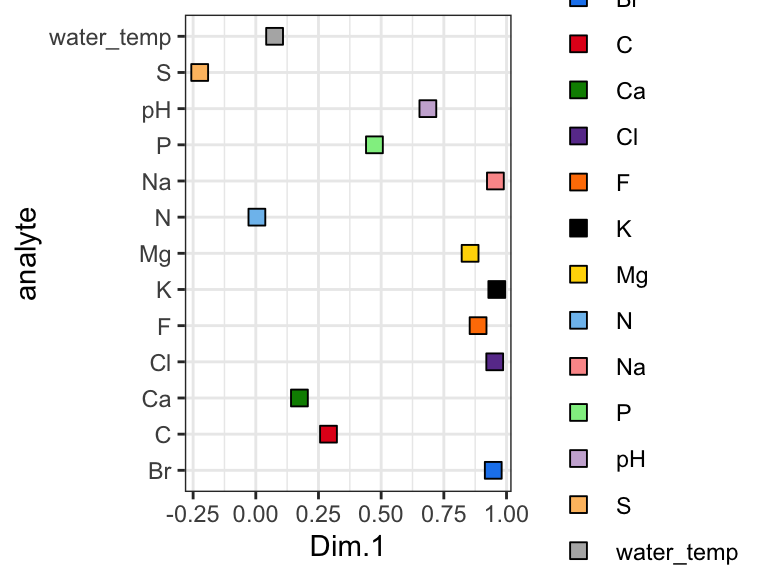
Cool! We can see that the first principal component retains nearly 50% of the variance in the original dataset, while the second dimension contains only about 20%. We can derive an important notion about PCA visualization from this: the scales on the two axes need to be the same for distances between points in the x and y directions to be comparable. This can be accomplished using coord_fixed() as an addition to your ggplots.
exercises
In this set of exercises, as you are filling out the runMatrixAnalysis() template, you can use the colnames() function to help you specify a long list of column names rather than typing them out by hand. For example, in the periodic table data set, we can refer to a set of columns (columns 10 through 20) with the following command:
colnames(periodic_table_subset)[10:20]
## [1] "electronegativity_pauling"
## [2] "first_ionization_poten_eV"
## [3] "second_ionization_poten_eV"
## [4] "third_ionization_poten_eV"
## [5] "electron_affinity_eV"
## [6] "atomic_radius_ang"
## [7] "ionic_radius_ang"
## [8] "covalent_radius_ang"
## [9] "atomic_volume_cm3_per_mol"
## [10] "electrical_conductivity_mho_per_cm"
## [11] "specific_heat_J_per_g_K"
colnames(periodic_table_subset)[c(18:20, 23:25)]
## [1] "atomic_volume_cm3_per_mol"
## [2] "electrical_conductivity_mho_per_cm"
## [3] "specific_heat_J_per_g_K"
## [4] "thermal_conductivity_W_per_m_K"
## [5] "polarizability_A_cubed"
## [6] "heat_atomization_kJ_per_mol"We can use that command in the template, as in the example below. With the notation colnames(periodic_table_subset)[c(5:7,9:25)], we can mark columns 5 - 7 and 9 - 25 as columns_w_values_for_single_analyte (note what happens when you run c(5:7,9:25) in the console, and what happens when you run colnames(periodic_table_subset)[c(5:7,9:25)] in the console). With the notation colnames(periodic_table_subset)[c(1:4, 8)] we can mark columns 1 - 4 and column 8 as columns_w_sample_ID_info (note what happens when you run c(1:4, 8) in the console, and what happens when you run colnames(periodic_table_subset)[c(1:4, 8)] in the console).
human metabolomics
For these questions, work with a dataset describing metabolomics data (i.e. abundances of > 100 different biochemicals) from each of 93 human patients, some of which have Chronic Kidney Disease. Your task is to discover a biomarker for Chronic Kidney Disease. This means that you will need to determine a metabolite whose abundance is strongly associated with the disease. To do this you should complete the following:
- Run a PCA analysis on
metabolomics_data(i.e.runMatrixAnalysis()withanalysis = "pca") - Plot the results of the analysis to determine which principal component (i.e. dimension) separates the healthy and kidney_disease samples.
- Obtain the ordination plot coordinates for the analytes in the PCA analysis (i.e.
runMatrixAnalysis()withanalysis = "pca_ord"). In your own words, how does this plot correspond to the original data set? - Visualize the ordination plot and determine which of the analytes are strongly associated with the principal component (i.e. dimension) separates the healthy and kidney_disease samples.
- Bingo! These analytes are associated with Chronic Kidney Disease and could be biomarkers for such.
- Complete this PCA analysis by creating a scree plot (i.e. use
analysis = "pca_dim"). In your own words, what does this plot mean?
grape vine chemistry
For this set of quesions, work with a dataset describing metabolomics data (i.e. abundances of > 100 different biochemicals) from 5 different wine grape varieties. Your task is to discover a biomarker for Chardonnay and a biomarker for Cabernet Sauvignon. This means that you will need to identify two metabolites, each of which are associated with one of those two grape varieties. To do this you should complete the following:
- Run a PCA analysis on
wine_grape_data(i.e.runMatrixAnalysis()withanalysis = "pca") - Plot the results of the analysis to determine which principal component (i.e. dimension) separates the Chardonnay samples from the other varieties and the Cabernet Sauvignon samples from the other varieties.
- Obtain the ordination plot coordinates for the analytes in the PCA analysis (i.e.
runMatrixAnalysis()withanalysis = "pca_ord"). In your own words, how does this plot correspond to the original data set? - Visualize the ordination plot and determine which of the analytes are strongly associated with the principal component (i.e. dimension) separates the Chardonnay samples from the other varieties and the Cabernet Sauvignon samples from the other varieties.
- Bingo! These analytes are associated with those varieites and could be biomarkers for such.
- Complete this PCA analysis by creating a scree plot (i.e. use
analysis = "pca_dim"). In your own words, what does this plot mean?
further reading
Here is a video that nicely explains PCA: https://www.youtube.com/watch?v=FgakZw6K1QQ&list=PLblh5JKOoLUIcdlgu78MnlATeyx4cEVeR
tsne and umap
set.seed(235)
runMatrixAnalysis(
data = metabolomics_data,
analysis = "pca",
column_w_names_of_multiple_analytes = NULL,
column_w_values_for_multiple_analytes = NULL,
columns_w_values_for_single_analyte = colnames(metabolomics_data)[c(3:126)],
columns_w_additional_analyte_info = NULL,
columns_w_sample_ID_info = colnames(metabolomics_data)[c(1:2)],
na_replacement = "mean"
) -> pca_data
## Replacing NAs in your data with mean
pca_data$technique <- "pca_data"
colnames(pca_data) <- gsub("\\.", "_", colnames(pca_data))
pca_data$Dim_1 <- as.numeric(scale(pca_data$Dim_1))
pca_data$Dim_2 <- as.numeric(scale(pca_data$Dim_2))
runMatrixAnalysis(
data = metabolomics_data,
analysis = "umap",
column_w_names_of_multiple_analytes = NULL,
column_w_values_for_multiple_analytes = NULL,
columns_w_values_for_single_analyte = colnames(metabolomics_data)[c(3:126)],
columns_w_additional_analyte_info = NULL,
columns_w_sample_ID_info = colnames(metabolomics_data)[c(1:2)],
na_replacement = "mean"
) -> umap_data
## Replacing NAs in your data with mean
umap_data$technique <- "umap_data"
umap_data$Dim_1 <- as.numeric(scale(umap_data$Dim_1))
umap_data$Dim_2 <- as.numeric(scale(umap_data$Dim_2))
runMatrixAnalysis(
data = metabolomics_data,
analysis = "tsne",
column_w_names_of_multiple_analytes = NULL,
column_w_values_for_multiple_analytes = NULL,
columns_w_values_for_single_analyte = colnames(metabolomics_data)[c(3:126)],
columns_w_additional_analyte_info = NULL,
columns_w_sample_ID_info = colnames(metabolomics_data)[c(1:2)],
na_replacement = "mean"
) -> tsne_data
## Replacing NAs in your data with mean
tsne_data$technique <- "tsne_data"
tsne_data$Dim_1 <- as.numeric(scale(tsne_data$Dim_1))
tsne_data$Dim_2 <- as.numeric(scale(tsne_data$Dim_2))
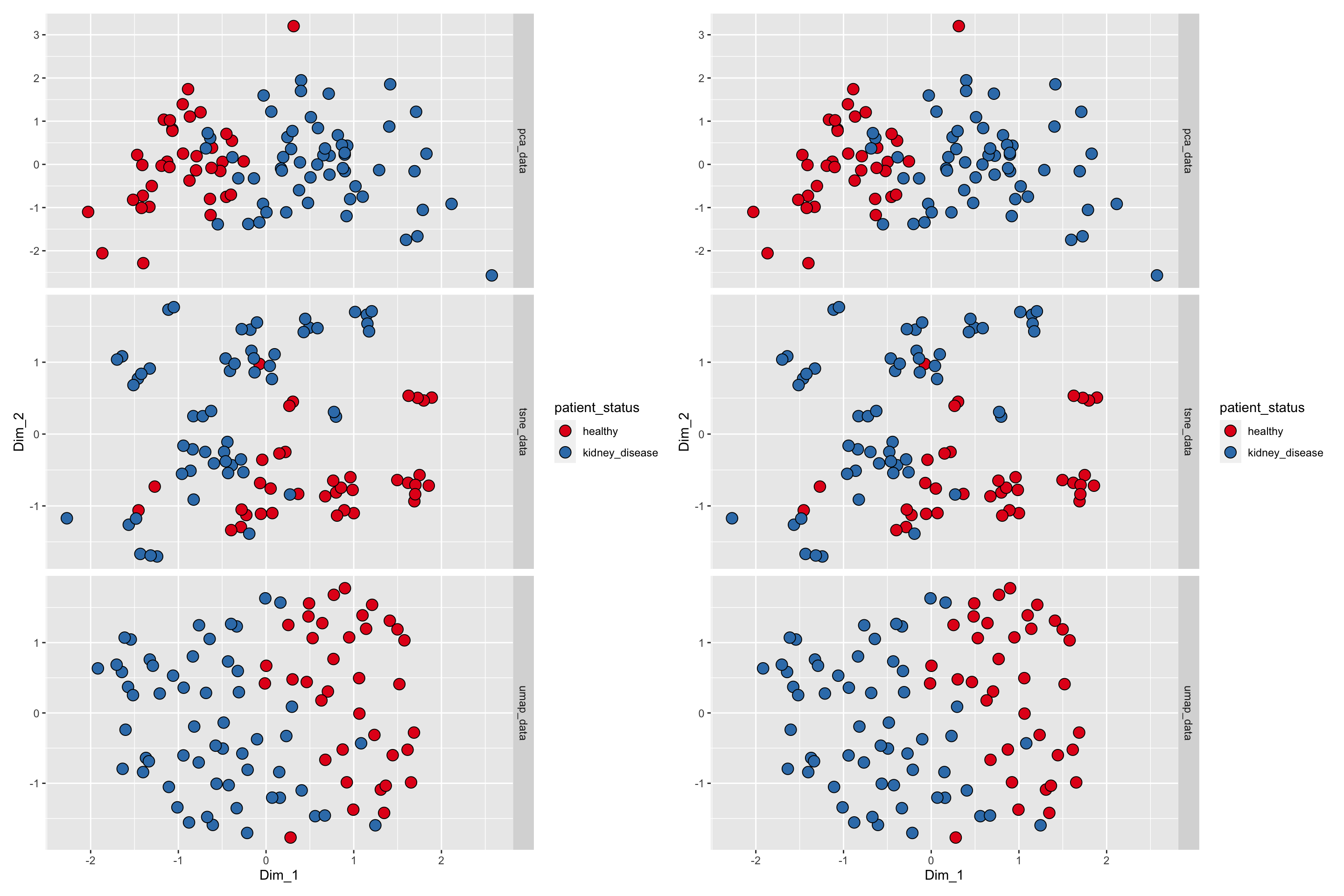
data <- rbind(pca_data, umap_data, tsne_data)
p1 <- ggplot(data) +
geom_point(aes(x = Dim_1, y = Dim_2, fill = patient_status), shape = 21, size= 4) +
facet_grid(technique~., scales = "free") +
scale_fill_brewer(palette = "Set1")
p2 <- ggplot(data) +
geom_point(aes(x = Dim_1, y = Dim_2, fill = patient_status), shape = 21, size= 4) +
facet_grid(technique~., scales = "free") +
scale_fill_brewer(palette = "Set1")
p1 + p2